Question

Find the curved surface area of a frustum of a cone. The slant height is 15cm, top and bottom diameter is 4 and 10cmm respectively.
(a) $350c{{m}^{2}}$
(b) $340c{{m}^{2}}$
(c) $345c{{m}^{2}}$
(d) $355c{{m}^{2}}$
(e) $315c{{m}^{2}}$

Answer 1

Hint: We start solving the problem by drawing the diagram to represent the frustum of the cone. We then find the curved surface of the cone using the formula $\pi rl$ and also the curved surface of frustum using this. We then find the length of the slant height of the cone using the given slant weight of the frustum given. We then substitute the values in the formula of a curved surface area to get the required result.

Complete step by step solution:
From above definition let the diagram of cone be curved surface area of right cone = $\pi rl$
Curved surface area of the small cone = $\pi {{r}_{1}}{{l}_{1}}$.
Curved surface area of frustum = $\pi rl-\pi {{r}_{1}}{{l}_{1}}$ .

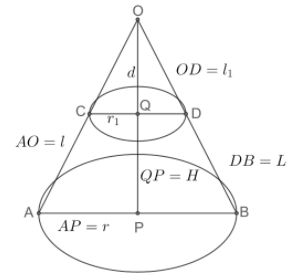
By the triangles OAB, OCD we can say that,
$\angle AOB\cong \angle COD$.
We can also say the relation given by $\angle OCD=\angle OAB$ as the lines CD, AB are parallel. By AA axiom the triangles are similar.
So, we can apply corresponding sides are in proportion:
$\dfrac{{{l}_{1}}}{l}=\dfrac{{{r}_{1}}}{r}..............\left( 1 \right)$.
From the figure we can say that ${{l}_{1}}=l-L$.
By substituting that into our equation (1) we get it as:
$\dfrac{l-L}{l}=\dfrac{{{r}_{1}}}{r}$.
$\Rightarrow 1-\dfrac{L}{l}=\dfrac{{{r}_{1}}}{r}$.
$\Rightarrow \dfrac{L}{l}=1-\dfrac{{{r}_{1}}}{r}$.
$\Rightarrow \dfrac{L}{l}=\dfrac{r-{{r}_{1}}}{r}$.
By simplifying, we can say the relation
 as:
$l=L\left( \dfrac{r}{r-{{r}_{1}}} \right).................\left( 2 \right)$.
The circumference of bases for both parts is assumed $S,{{S}_{1}}$ . We can say $S=2\pi r,{{S}_{1}}=2\pi {{r}_{1}}$ .
From figure we can say that, the curved surface are:
Curved surface area of frustum =$\dfrac{1}{2}\left( Sl-{{S}_{1}}{{l}_{1}} \right)$.
By substituting $S,{{S}_{1}}$ into equation, we get it as:
Curved surface area =$\dfrac{1}{2}\times 2\pi rl-\dfrac{1}{2}\times 2\pi {{r}_{1}}{{l}_{1}}$.
By substituting l as equation (2), we get it as
Curved surface area \[=\pi r\times L\left( \dfrac{r}{r-{{r}_{1}}} \right)-\pi {{r}_{1}}{{l}_{1}}\]
Substituting ${{l}_{1}}=l-L\Rightarrow L\left( \dfrac{r}{r-{{r}_{1}}} \right)-L$, we have
\[\begin{align}
  & \Rightarrow \pi L\left( \dfrac{{{r}^{2}}}{r-{{r}_{1}}} \right)-\pi {{r}_{1}}\left[ L\left( \dfrac{r}{r-{{r}_{1}}} \right)-L \right] \\
 & \Rightarrow \pi L\left( \dfrac{{{r}^{2}}}{r-{{r}_{1}}} \right)-\pi {{r}_{1}}L\left( \dfrac{r}{r-{{r}_{1}}}-1 \right) \\
 & \Rightarrow \pi L\left( \dfrac{{{r}^{2}}}{r-{{r}_{1}}} \right)-\pi {{r}_{1}}L\left( \dfrac{{{r}_{1}}}{r-{{r}_{1}}} \right) \\
 & \Rightarrow \pi L\left( \dfrac{{{r}^{2}}}{r-{{r}_{1}}} \right)-\pi L\left( \dfrac{{{r}_{1}}^{2}}{r-{{r}_{1}}} \right) \\
 & \Rightarrow \pi L\left( \dfrac{{{r}^{2}}-{{r}_{1}}^{2}}{r-{{r}_{1}}} \right) \\
 & \Rightarrow \pi L\left( \dfrac{\left( r+{{r}_{1}} \right)\left( r-{{r}_{1}} \right)}{r-{{r}_{1}}} \right) \\
\end{align}\]
By cancelling common terms, we get its value as:
Curved surface area =$\pi L\left( r+{{r}_{1}} \right)$.
By multiplying 2 and dividing 2 we get it as
Curved surface area =$\dfrac{\pi L}{2}\left( 2r+2{{r}_{1}} \right)=\dfrac{\pi L}{2}\left( d+{{d}_{1}} \right)$.
Where $d,{{d}_{1}}$ are diameter. By substituting given value in question.
$\pi =3,L=15,d=10,{{d}_{1}}=4$ we get it as:
Curved surface area =$\dfrac{3\times 15}{2}\left( 10+4 \right)=\dfrac{3\times 15\times 14}{2}$.
By simplifying, we get it as:
Curved surface area = $3\times 15\times 7=315c{{m}^{2}}$.
Therefore option (c) is the correct answer.

Note: Alternatively, we can solve the formula by using the formula of curved surface area of the frustum directly.
We know that the curved surface area of the frustum is $A=\pi \left( r+{{r}_{1}} \right)l$.
$\Rightarrow A=\left( 3 \right)\times \left( 2+5 \right)\times \left( 15 \right)$.
$\Rightarrow A=\left( 45 \right)\times \left( 7 \right)$.
$\Rightarrow A=375c{{m}^{2}}$.
We should not make calculation mistakes while solving this problem. If we don’t know the formula of the area and volume of the frustum, we can estimate by subtracting from the cone as we did in this problem.