Question

Find the coordinates of the centroid of the triangle if point D (-7, 6), E (5, 8) and F (2, -2) are the midpoints of the sides of that triangle.

Answer 1

Hint: We will use the very important concept that if we have a triangle ABC and D, E and F are the midpoints of BC, CA and AB respectively, then centroid of triangle ABC coincides with the centroid of triangle DEF by using the centroid formula which is as follows:
If \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)\] are the vertices of triangle, then the centroid of triangle is \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]

Complete step-by-step answer:


We have been given the midpoint of sides of the triangle as D (-7, 6), E (5, 8) and F (2, -2).
Let us suppose the triangle to be ABC and D, E and F are the midpoints of BC, AC and AB.

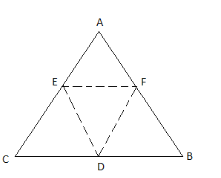
Now we know that if we have any triangle ABC and their midpoint’s area D, E and F then the centroid of triangle ABC coincides with the centroid of triangle DEF.
So we will find the centroid of triangle DEF which gives the centroid of triangle ABC.
We know that if \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)\] are the vertices of the triangle, then,
X coordinate of centroid \[=\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3}\]
Y coordinate of centroid \[=\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3}\]
We have D (-7, 6), E (5, 8) and F (2, -2)
X coordinate of centroid of triangle DEF \[=\dfrac{-7+5+2}{3}=\dfrac{0}{3}=0\]
Y coordinate of centroid of triangle DEF \[=\dfrac{6+8+(-2)}{3}=\dfrac{14-2}{3}=\dfrac{12}{3}=4\]
So the coordinates of the centroid of the triangle DEF are (0, 4)
Hence the coordinates of the centroid of the triangle ABC are (0, 4).

Note: Be careful while finding the values of the coordinates of the centroid and also take care of the sign while substituting the values of coordinates of the given midpoints. Also, remember that the centroid of a triangle is a point where all the three medians of the triangle intersect and the median is a line that joins the midpoint of a side and the opposite vertex of a triangle.