Question

Find the area of the triangle with sides 5cm, 12 cm and 13cm.

Answer 1

Hint: As we are asked to find the area of the triangle, we first need to find the semi-perimeter s of the triangle which is equal to half of the perimeter of the triangle, i.e., $s=\dfrac{a+b+c}{2}$ . Once you get the value of s, use the herons’ formula for the area of the triangle $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to get the answer.

Complete step-by-step answer:
Let us first draw the diagram of the situation given in the question for better visualisation.

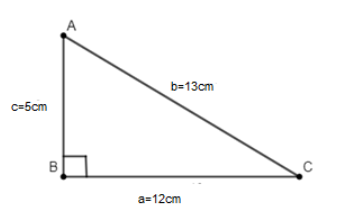
Now as we are asked to find the area of the $\Delta ABC$ using herons’ formula, we will first find the semi-perimeter s of the triangle which is equal to half of the perimeter of the triangle, i.e., $s=\dfrac{a+b+c}{2}$ . According to the figure, a=12cm, b=13cm and c=5cm.
$s=\dfrac{a+b+c}{2}=\dfrac{12+13+5}{2}=15$
Now we will use the herons’ formula, according to which area of a triangle with sides a, b and c is given by $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ .
\[\text{Area of }\Delta \text{ABC}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}=\sqrt{15\left( 15-12 \right)\left( 15-13 \right)\left( 15-5 \right)}\]
$\Rightarrow \text{Area of }\Delta \text{ABC}=\sqrt{15\times 3\times 2\times 10}=\sqrt{3\times 5\times 3\times 2\times 2\times 5}=5\times 3\times 2=30$
Therefore, the area of the triangle given in the question is 30 sq cm.

Note:Remember that herons’ formula is valid for all the triangles with sides given. Also, if not mentioned in the question, never use herons’ formula for right angles triangles, as you can directly use the formula $area=\dfrac{1}{2}\times b\times h$ for a right angled triangle with given sides. As for the above question, base is a=12 and height is c=5. So, area is $area=\dfrac{1}{2}\times 5\times 12=30\text{uni}{{\text{t}}^{2}}$ , which is the correct answer and is easy to calculate as well, and we can use this because the triangle is right angled as its sides form a Pythagorean triplet (5,12,13).