Question

Find the area of the trapezium \[ABCD\] in which \[AB||DC\] , \[AB=18\text{ cm}\] , \[\angle B=\angle C={{90}^{\circ }}\] , \[CD=\text{12 cm}\] and \[AD=\text{10 cm}\].

Answer 1

Hint: Finding the area of a figure using the formula of the trapezium. Moreover, we can also calculate the area of a trapezium by addition of area of triangle and area of rectangle.

Complete step-by-step answer:

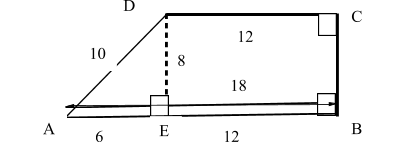
So first, we will draw a rough sketch from the given date , that is,...
\[\begin{gathered}
  & ABCD \\
 & AB||DC \\
 & AB=18\text{ cm} \\
 & \angle B=\angle C={{90}^{\circ }} \\
 & CD=\text{12 cm} \\
 & AD=\text{10 cm} \\
\end{gathered}\]
So, now all we are missing is the distance between the parallel lines. This is to calculate that we will assume a point E which makes an angle \[{{90}^{\circ }}\] with the line segment AB. Basically mean, that this point E will make a perpendicular line to the line segment AB with the other point of this perpendicular lying on point D.
The line AE will be of length (\[AE=AB-EB\])because from the figure we can conclude that \[EBCD\] is a rectangle thus \[\,[EB=CD\,\,;\,BC=ED\,\,\,rec\tan gle\text{EBCD}]\]..
\[\begin{gathered}
  & AB=AE+EB \\
 & AE=AB-EB \\
 & AE=18-12=6cm\,\,\,\,\,\,\,\,\,[EB=CD\,\,;\,BC=ED\,\,\,rec\tan gle\text{EBCD}] \\
\end{gathered}\]
Now, since \[\vartriangle AED\] is a right angled triangle with angle \[\angle AED={{90}^{\circ }}\] .we will use the Pythagoras theorem formula and find the height of this right angled triangle.

\[\begin{gathered}
  & {{(AD)}^{2}}={{(AE)}^{2}}+{{(ED)}^{2}}\,\,\,\,\text{ }\!\![\!\!\text{ pythagoras }\!\!]\!\!\text{ } \\
 & \text{1}{{\text{0}}^{2}}=E{{D}^{2}}+{{6}^{2}} \\
 & ED=\sqrt{100-36}=8\,\text{cm}\text{.} \\
 & \text{ED=distance between parallel lines} \\
\end{gathered}\]

So now we get the height of the \[\vartriangle AED\] which is also the distance between the two parallel sides of the triangle. Thus, we will now use the formula to find the area of the trapezium....
\[\begin{gathered}
  & \text{Area of trapezium}=\dfrac{1}{2}\times \text{Sum of parallel sides}\times \text{distance between the}\,\text{parallel lines} \\
 & \text{Area of trapezium}=\dfrac{1}{2}\times (AB+EB)\times (ED) \\
 & \text{Area of trapezium}=\dfrac{1}{2}\times (18+12)\times (8) \\
 & \text{Area of trapezium}=\dfrac{1}{2}\times (30)\times 8 \\
 & \text{Area of trapezium}=120\,\,\,\text{c}{{\text{m}}^{2}}. \\
\end{gathered}\]

Thus the area is 120 square centimetre.

Note: The \[\,\text{c}{{\text{m}}^{2}}\] given here is square centimetre and the \[\text{cm}\] used here is the centimetre in length. From the diagram we can also use the addition of the area of \[\vartriangle AED\] and area of \[rec\tan gle\text{EBCD}\] to find the area of the trapezium. The area of trapezium depends on its parallel sides and distance between the parallel sides. If we know the length of parallel sides and the distance between them, then we can easily find the area of trapezium.