Question

Find the area of the sector whose arc length and radius are 16 cm and 9 cm respectively.

Answer 1

Hint: First of all, use the formula \[r\theta \] for the arc length of the circle. Here, substitute the value of the arc length and radius to get the value of \[\theta \]. Now, substitute the value of \[\theta \] in \[\dfrac{{{r}^{2}}\theta }{2}\] to get the area of the sector of the circle.

Complete step-by-step answer:

In this question, we have to find the area of the sector whose arc length and radius are 16 cm and 9 cm respectively. First of all, let us see what an arc and sector is

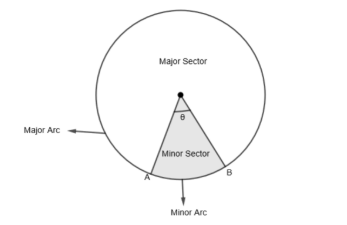
Arc: An arc of the circle is a part of it. It is the fraction of the circumference of the circle. In the above diagram, the bigger arc joining AB is the major arc and the smaller arc joining AB is the minor arc.
Sector: A sector is a part of a circle enclosed between two radii. In the above diagram, the shaded portion is the minor sector and the unshaded portion is the major sector.
Now, let us consider our question. We are given that the radius of the circle is 16cm and the length is 9 cm.

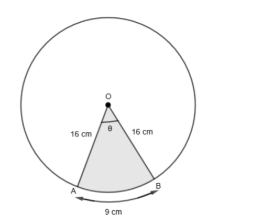
In the above figure, OA = OB = radius = 16 cm and AB is arc length that is 9 cm.
We know that the length of the arc of the circle = \[r\theta \] where r is the radius of the circle and \[\theta \] is the angle of the sector. So, we get,
\[r\theta =9cm\]
By substituting the values of r = 16 cm, we get,
\[\left( 16cm \right)\theta =9cm\]
\[\theta =\dfrac{9}{16}rad\]
Now, we know that in a circle, the sector is given by \[\dfrac{{{r}^{2}}\theta }{2}\].
By substituting the value of r = 16 cm and \[\theta =\dfrac{9}{16}rad\], we get,
Area of the sector of the circle \[=\dfrac{{{\left( 16 \right)}^{2}}}{2}\left( \dfrac{9}{16} \right)\]
\[=\dfrac{16\times 16\times 9}{2\times 16}\]
\[=8\times 9=72c{{m}^{2}}\]
So, we get the area of the sector as \[72c{{m}^{2}}\].

Note: In this question, students must note that \[\theta \] must be in radians. In case, we have \[\theta \] in degrees, we first change it in radians by multiplying it by \[\dfrac{{{180}^{o}}}{\pi }\]. Also, students must note that \[\theta \] is a dimensionless quantity, so all the units of the dimensions in a formula must be the same. Also, in this question, students must not concern themselves with whether the arc or the sector is minor or major.