Question

Find the area of the region included between the parabola \[{{y}^{2}}=3x\]and the circle \[{{x}^{2}}+{{y}^{2}}-6x=0\], lying in the first quadrant.

Answer 1

Hint: In this question, we first need to draw the diagram to get a clear picture of the region that we have to calculate the area. Then find the intersection points of the two curves which gives the limits within which they need to be integrated. Now, on subtracting the parabola from the circle and integrating within the limits gives the result.

Complete step-by-step answer:
Now, from the given equations of circle and parabola in the question we have
\[\begin{align}
  & {{y}^{2}}=3x \\
 & {{x}^{2}}+{{y}^{2}}-6x=0 \\
\end{align}\]
Let us now solve these two equations to get the point of intersection
\[\Rightarrow {{x}^{2}}+3x-6x=0\]
Now, on rearranging the terms we get,
\[\Rightarrow {{x}^{2}}=3x\]
Now, on further simplification we get,
\[\Rightarrow x=0,3\]
Let us now substitute back this value of x to get y
\[\Rightarrow {{y}^{2}}=3x\]
Now, on substituting \[x=0\]we get,
\[\begin{align}
  & \Rightarrow {{y}^{2}}=0 \\
 & \Rightarrow y=0 \\
\end{align}\]
Now, on substituting \[x=3\]we get,
\[\begin{align}
  & \Rightarrow {{y}^{2}}=3\times 3 \\
 & \Rightarrow {{y}^{2}}=9 \\
\end{align}\]
Now, on further simplification we get,
\[\Rightarrow y=\pm 3\]
Here, as we need to find the area in the first quadrant so we consider
\[\therefore \left( x,y \right)=\left( 0,0 \right),\left( 3,3 \right)\]

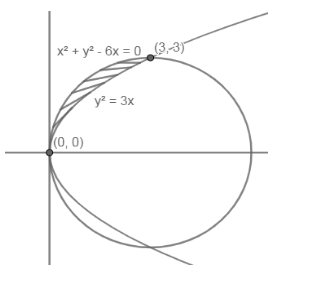
As we already know from the applications of integration that
The space occupied by the curve along with the axis, under the given condition is called area of bounded region.
Area bounded by two curves \[y=f\left( x \right)\] and \[y=g\left( x \right)\] in which \[f\left( x \right)\] lies above \[g\left( x \right)\]between \[x=a\]and \[x=b\] is given by
\[\Rightarrow \int\limits_{a}^{b}{\left\{ f\left( x \right)-g\left( x \right) \right\}dx}\]
From, the given circle equation we have
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-6x=0\]
Now, on rearranging we get,
\[\Rightarrow {{y}^{2}}=6x-{{x}^{2}}\]
Now, by applying square root we get,
\[\Rightarrow y=\sqrt{6x-{{x}^{2}}}\]
Similarly, from the given equation of parabola we have
\[\Rightarrow y=\sqrt{3x}\]
Now, on comparing these with the formula we get,
\[\begin{align}
  & f\left( x \right)=\sqrt{6x-{{x}^{2}}} \\
 & g\left( x \right)=\sqrt{3x} \\
 & a=0,b=3 \\
\end{align}\]
Now, by substituting the respective values in the formula we get,
\[\Rightarrow \int\limits_{a}^{b}{\left\{ f\left( x \right)-g\left( x \right) \right\}dx}\]
\[\Rightarrow \int\limits_{0}^{3}{\left\{ \sqrt{6x-{{x}^{2}}}-\sqrt{3x} \right\}dx}\]
Now, this can also be written further as
\[\Rightarrow \int\limits_{0}^{3}{\left\{ \sqrt{{{3}^{2}}-{{\left( x-3 \right)}^{2}}}-\sqrt{3x} \right\}dx}\]
As we already know from the formulae of integration that
\[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\]
\[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\dfrac{1}{2}\left[ x\sqrt{{{a}^{2}}-{{x}^{2}}}+{{a}^{2}}{{\sin }^{-1}}\left( \dfrac{x}{a} \right) \right]\]
Now, by using this formula we get,
\[\dfrac{1}{2}\left[ \left( x-3 \right)\sqrt{{{3}^{2}}-{{\left( x-3 \right)}^{2}}}+{{3}^{2}}{{\sin }^{-1}}\left( \dfrac{x-3}{3} \right) \right]_{0}^{3}-\sqrt{3}\left( \dfrac{2}{3}{{x}^{\dfrac{3}{2}}} \right)_{0}^{3}\]
Now, on further substituting the limits we get,
\[\Rightarrow \dfrac{1}{2}\left[ \left( 3-3 \right)\sqrt{{{3}^{2}}-{{\left( 3-3 \right)}^{2}}}+{{3}^{2}}{{\sin }^{-1}}\left( \dfrac{3-3}{3} \right)-\left( 0-3 \right)\sqrt{{{3}^{2}}-{{\left( 0-3 \right)}^{2}}}-{{3}^{2}}{{\sin }^{-1}}\left( \dfrac{0-3}{3} \right) \right]-\sqrt{3}\left( \dfrac{2}{3}{{3}^{\dfrac{3}{2}}}-\dfrac{2}{3}{{0}^{\dfrac{3}{2}}} \right)\]
Now, on further simplification by writing the terms that are 0 we get,
\[\Rightarrow \dfrac{1}{2}\left[ 0-\left( 0-3 \right)\sqrt{{{3}^{2}}-{{\left( 0-3 \right)}^{2}}}-{{3}^{2}}{{\sin }^{-1}}\left( \dfrac{0-3}{3} \right) \right]-\sqrt{3}\left( \dfrac{2}{3}{{3}^{\dfrac{3}{2}}}-0 \right)\]
Now, this can be further written in the simplified form as
\[\Rightarrow \dfrac{1}{2}\left[ 3\sqrt{9-9}-9{{\sin }^{-1}}\left( -1 \right) \right]-\sqrt{3}\left( 2\sqrt{3} \right)\]
Now, on further simplification we get,
\[\Rightarrow \dfrac{1}{2}\left[ -9\left( \dfrac{-\pi }{2} \right) \right]-2\times 3\text{ }\left[ \because {{\sin }^{-1}}\left( -1 \right)=\dfrac{-\pi }{2} \right]\]
Now, on further simplifying the terms in the above expression we get,
\[\Rightarrow \dfrac{9\pi }{4}-6\]

Note: Instead of integrating with respect to x in the given coordinates we can also calculate it by integrating it with respect to y from the values of the y obtained in the coordinates. Bth the integration would be difficult.It is important to note that while finding the coordinates we should be careful of calculation mistakes. Then while doing the integration we should not neglect any of the terms and while substituting the limits we need to be careful about the sign because it changes the result completely.