Question

Find the area of the region bounded by the curve $y={{x}^{3}}$, the lines y = 0, x= 2 and x=4.

Answer 1

Hint: Plot the graph on a graph. Identify the region whose area is to be found. Use the fact that the area of the region bounded by y=f(x), the x-axis and the ordinates x = a and x= b is given by
$y=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$. Hence argue that the required area is given by $A=\int_{2}^{4}{{{x}^{3}}}dx$. Integrate and hence find the required area.

Complete step-by-step answer:

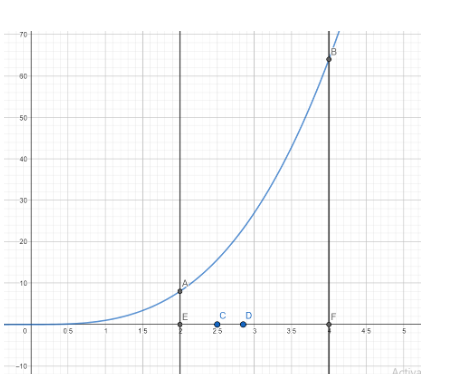
Hence the area bounded by the curve $y={{x}^{3}}$, the lines y = 0, x= 2 and x= 4 is the area of the region AECDFBA.
This is the region bounded by the curve $y={{x}^{3}}$, the x-axis and the ordinates x= 2 and x= 4.
We know that the area of the region bounded by y=f(x), the x-axis and the ordinates x = a and x= b is given by
$y=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$.
Hence the required area $=\int_{2}^{4}{\left| {{x}^{3}} \right|dx}$
We know that $x\in \left( 2,4 \right)\Rightarrow {{x}^{3}}\ge 0$
Hence, we have
Required area $=\int_{2}^{4}{{{x}^{3}}dx}$
We know that $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}$ and according to the first fundamental theorem of calculus if F’(x) = f(x), then $\int_{a}^{b}{f\left( x \right)dx}=F\left( b \right)-F\left( a \right)$
Hence, we have
Required area $=\left. \dfrac{{{x}^{4}}}{4} \right|_{2}^{4}=\dfrac{256}{4}-\dfrac{16}{4}=64-4=60$
Hence the required area is 60 square units.

Note: Alternative Solution:
The area bounded by the curve $y={{x}^{n}}$, the x-axis and the ordinates x= a, and x= b, $a,b\ge 0$ is given by
$\dfrac{{{b}^{n+1}}-{{a}^{n+1}}}{n+1}$
Hence the required area $=\dfrac{{{4}^{4}}-{{2}^{4}}}{4}=\dfrac{256-16}{4}=\dfrac{240}{4}=60$ square units.