Question

How do you find the area of one petal of \[r = 2\cos (3\theta )\] ?

Answer 1

Hint: Here in this we have to find the area of one petal of \[r = 2\cos (3\theta )\] . To find the area we use formula \[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } \] , where \[\alpha \] and \[\beta \] are the limit points. Hence by substituting all the values in the formula and then by simplifying we obtain the area of one petal.

Complete step-by-step answer:
In general let us consider \[r = a\sin (n\theta )\] or \[r = a\sin (n\theta )\] where \[a \ne 0\] and n is a positive number greater than 1. For the graph of rose if the value of n is odd then rose will have n petals or if the value of n is even then the rose will have 2n petals. Here “a” represents the radius of the circle where the rose petals lie.
Now consider the given equation \[r = 2\cos (3\theta )\] . Here a=2, the radius of the circle is 2 and n=3, the number is odd so we have 3 petals for the rose.
The figure is as shown

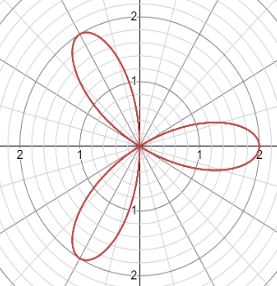
To find the area we use the formula \[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } \] ------- (1)
Here the limits points are not given. Therefore, we have to find the value of \[\alpha \] and \[\beta \]
Now consider the given equation \[r = 2\cos (3\theta )\] ------- (2)
Substitute r=0 in equation (2) we have
 \[ \Rightarrow 0 = 2\cos (3\theta )\]
This is written as
 \[ \Rightarrow 0 = \cos (3\theta )\]
By taking the inverse we have
 \[ \Rightarrow {\cos ^{ - 1}}(0) = 3\theta \]
By the table of trigonometry ratios for standard angles in radians we have \[\cos \left( {\dfrac{\pi }{2}} \right) = 1\] so we have
 \[ \Rightarrow \dfrac{\pi }{2} = 3\theta \]
Dividing by 3 on the both sides we have
 \[ \Rightarrow \theta = \dfrac{\pi }{6}\]
Therefore \[\left( {\alpha ,\beta } \right) = \left( {r,\theta } \right) = \left( {0,\dfrac{\pi }{6}} \right)\] ----------- (3)
Substituting equation (2) and equation (3) in equation (1) we have
 \[A = 2 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {{{(2\cos (3\theta ))}^2}d\theta } \]
Applying square, we have
 \[ \Rightarrow A = 2 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {\left( {4{{\cos }^2}(3\theta )} \right)d\theta } \]
On simplifying we have
 \[ \Rightarrow A = 4\int_0^{\dfrac{\pi }{6}} {\left( {{{\cos }^2}(3\theta )} \right)d\theta } \]
Apply the half angle formula for the cosine function we have
 \[ \Rightarrow A = 4\int_0^{\dfrac{\pi }{6}} {\left( {\dfrac{{1 + \cos (6\theta )}}{2}} \right)d\theta } \]
On simplifying we have
 \[ \Rightarrow A = 4 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {\left( {1 + \cos (6\theta )} \right)d\theta } \]
Take integral to each term we have
 \[ \Rightarrow A = 2\left( {\int_0^{\dfrac{\pi }{6}} {d\theta } + \int_0^{\dfrac{\pi }{6}} {\cos (6\theta )d\theta } } \right)\]
On applying the integration, we have
 \[ \Rightarrow A = 2\mathop {[\theta ] }\nolimits_0^{\dfrac{\pi }{6}} + 2\left[ {\dfrac{{\sin (6\theta )}}{6}} \right] _0^{\dfrac{\pi }{6}}\]
Applying the limit points, we get
 \[ \Rightarrow A = 2\left[ {\dfrac{\pi }{6} - 0} \right] + \dfrac{2}{6}\left[ {\sin 6\left( {\dfrac{\pi }{6}} \right) - \sin (0)} \right] \]
On simplifying we get
 \[
   \Rightarrow A = \dfrac{\pi }{3} + \dfrac{1}{3}\left[ {0 - 0} \right] \\
   \Rightarrow A = \dfrac{\pi }{3}sq.units \;
 \]
Therefore, the area of one petal of \[r = 2\cos (3\theta )\] is \[\dfrac{\pi }{3}\;sq.units\]
So, the correct answer is “ \[\dfrac{\pi }{3}\;sq.units\] ”.

Note: The area of a petal for the circle for the polar coordinates is given by \[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } \] . The unit for the area is given as a square unit. In the polar form the coordinates are represented in the form of \[\left( {r,\theta } \right)\] where r represents the radius of the circle and the \[\theta \] represents the angle.