Question

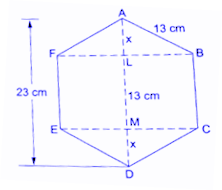
Find the area of a regular hexagon $ABCDEF$ in which each side measures $13cm$ and whose height is $23cm$ as shown in figure.

Answer 1

Hint: Use Pythagoras Theorem and Area of trapezium $ = \dfrac{1}{2} \times (\text{sum}\ \text{of}\ \text{parallel}\ \text{sides}) \times height$ to find the area of the regular hexagon .(As if we divide the hexagon then trapezium and triangle will form).
Complete step-by-step solution -
According to question it is given ,
A regular hexagon $ABCDEF$, where
$
  AB = BC = CD = DE = EF = FA = 13cm \\
  AD = 23cm \\
 $
Here $AL = MD$
Therefore Let $AL = MD = x$
Here $AD = AL + LM + MD$
$
   \Rightarrow 23 = 13 + 2x \\
   \Rightarrow 2x = 23 - 13 = 0 \\
   \Rightarrow x = 5 \\
 $
Now, In $\Delta ABL$using Pythagoras Theorem , we get
$
   \Rightarrow A{B^2} = A{L^2} + L{B^2} \\
   \Rightarrow {13^2} = {x^2} + L{B^2} \\
   \Rightarrow 169 = 25 + L{B^2} \\
   \Rightarrow L{B^2} = 169 - 25 = 144 \\
   \Rightarrow LB = 12 \\
 $
By the symmetry
Here the area of $(Trap.ABCD) = $area of $(Trap.AFED)$
Therefore,
$ \Rightarrow $Area $(Hex.ABCDEF) = 2 \times $area of $(Trap.ABCD)$
$ \Rightarrow $Area of trapezium $ = \dfrac{1}{2} \times (\text{sum}\ \text{of}\ \text{parallel}\ \text{sides}) \times height$
$ \Rightarrow $Area $(Trap.ABCD) = $$\dfrac{1}{2} \times (BC + AD) \times LB$
$ \Rightarrow $ Area $(Trap.ABCD) = $$\dfrac{1}{2} \times (13 + 23) \times 12 = 216c{m^2}$
$\therefore $Area $(Hex.ABCDEF) = 2 \times $area of $(Trap.ABCD)$$ = 2 \times 216 = 432c{m^2}$
$\therefore $Area $(ABCDEFGH) = 432c{m^2}$
Note: It is always advisable to draw the figure before starting the solution and if there is a hexagon who doesn't have a formula of finding area , we can divide the figure in such a way that the shapes that are formed will be known and their formulas of finding area are also known .