Question

Find the area bounded by \[y = {x^2} - 4x + 3\], x –axis, y-axis and the tangent to the curve at point \[\dfrac{5}{2}\].

Answer 1

Hint: In this question, we have to find out the bounded region for the particular given. First we need to find the equation of the tangent with the help of the given equation and then using the formula for a bounded region we will get the area bounded by the given particulars.

Formula used: To find the slope m of a curve at a particular point, we differentiate the equation of the curve. If the given curve is y=f(x) we evaluate \[\dfrac{{dy}}{{dx}}\] or f’(x) and substitute the value of x to find the slope.
Then the tangent at \[\left( {{x_1},{y_1}} \right)\] is \[y - {y_1} = m\left( {x - {x_1}} \right)\].
Differentiation formula:\[\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{n - 1}}\]
The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. i.e.\[\int\limits_a^b {f(x)dx} \] \[\]
\[\int\limits_a^b {{x^n}dx} = \left. {\dfrac{{{x^{n + 1}}}}{{n + 1}}} \right|_a^b\]

Complete step-by-step answer:
We have to find out the area bounded by \[y = {x^2} - 4x + 3\], x -axis, y-axis and the tangent to the curve at point \[\dfrac{5}{2}\].
First we need to find out the tangent line.
Here x= \[\dfrac{5}{2}\]
Thus by substituting the value of x in the given equation we get, \[y = {\left( {\dfrac{5}{2}} \right)^2} - 4 \times \dfrac{5}{2} + 3\]
\[y = \dfrac{{25}}{4} - 10 + 3\]
By solving the above equation we get,
\[y = \dfrac{{25}}{4} - 7\]
\[ \Rightarrow y = \dfrac{{25 - 28}}{4} = - \dfrac{3}{4}\]
Let us now differentiate the given curve with respect to x, we have,
\[\Rightarrow \dfrac{{dy}}{{dx}} = 2x - 4\]
Hence the slope of the tangent line is
\[\Rightarrow {\left. {\dfrac{{dy}}{{dx}}} \right|_{x = \dfrac{5}{2}}} = 2 \times \dfrac{5}{2} - 4 = 5 - 4 = 1\]
By substituting the slope in the equation of tangent we get
The equation of the tangent \[ = y - \left( { - \dfrac{3}{4}} \right) = 1\left( {x - \dfrac{5}{2}} \right)\]
On solving the above equation we get,
\[\Rightarrow y + \dfrac{3}{4} = x - \dfrac{5}{2}\]
\[\Rightarrow y = x - \left( {\dfrac{5}{2} + \dfrac{3}{4}} \right)\]
On further solving we find the equation with respect to y,
\[\Rightarrow y = x - \dfrac{{10 + 3}}{4}\]
\[\Rightarrow y = x - \dfrac{{13}}{4}\]

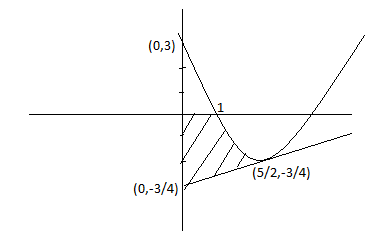
The above graph represents the area to be founded.
Therefore the area bounded by \[y = {x^2} - 4x + 3\], x -axis, y-axis and the tangent to the curve at point \[\dfrac{5}{2}\]is\[\int\limits_{x = 0}^{x = \dfrac{5}{2}} {\left[ {\left( {{x^2} - 4x + 3} \right) - \left( {x - \dfrac{{13}}{4}} \right)} \right]} dx\]
Let us solve the equation inside the integral we get,
The area bounded by the given curve\[ = \int\limits_0^{\dfrac{5}{2}} {\left( {{x^2} - 5x + 3 + \dfrac{{13}}{4}} \right)} dx\]
Let us now integrate the above equation we get,
\[ = \left. {\dfrac{{{x^3}}}{3}} \right|_0^{\dfrac{5}{2}} - \left. {5\dfrac{{{x^2}}}{2}} \right|_0^{\dfrac{5}{2}} + \dfrac{{12 + 13}}{4}\left. x \right|_0^{\dfrac{5}{2}}\]
Let us substitute the upper and lower limit we get,
The area bounded by the curve\[ = \dfrac{1}{3}\left[ {{{\left( {\dfrac{5}{2}} \right)}^3} - 0} \right] - \dfrac{5}{2}\left[ {{{\left( {\dfrac{5}{2}} \right)}^2} - 0} \right] + \dfrac{{25}}{4}\left( {\dfrac{5}{2} - 0} \right)\]
On further solving we get,
\[ = \dfrac{1}{3} \times \dfrac{{125}}{8} - \dfrac{5}{2} \times \dfrac{{25}}{4} + \dfrac{{25}}{4} \times \dfrac{5}{2}\]
The area bounded by the given curve=\[\dfrac{{125}}{{24}}\] sq. unit.

Hence, the area bounded by \[y = {x^2} - 4x + 3\], x -axis, y-axis and the tangent to the curve at point \[\dfrac{5}{2}\] is \[\dfrac{{125}}{{24}}\]sq. unit.

Additional Information: To determine the equation of a tangent to a curve:
Find the derivative using the rules of differentiation.
Substitute the x-coordinate of the given point into the derivative to calculate the gradient of the tangent.
Substitute the gradient of the tangent and the coordinates of the given point into an appropriate form of the straight line equation that is \[y - {y_1} = m\left( {x - {x_1}} \right)\] where m is the gradient of the tangent and \[\left( {{x_1},{y_1}} \right)\]is the point.

Note: We should consider the given point to find the corresponding point because it will lead us to the equation of the tangent line. Suppose we do not find the corresponding point we cannot find the equation of tangent which will not lead to a bound for the given equation.