Question

Find the area bounded by \[y = x + \sin x\] and its inverse between \[x = 0\] and \[x = 2\pi \].
A) 2
B) 4
C) 6
D) 8

Answer 1

Hint:
Here, we will use the concept of integration to find the area bounded by the curves. First we will find the point of inflection and then integrate the curves to find the area. Integration is the process of adding small areas to find the whole area.
Formula Used: Area between two curves which intersect each other at \[\left[ {a,b} \right]\] is given by \[\int_a^c {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx + \int_c^b {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \]

Complete step by step solution:
We are given with a function \[y = x + \sin x\].
Replacing the function \[y\]with \[f\left( x \right)\] , we get
\[ \Rightarrow f\left( x \right) = x + \sin x\]
Here, \[x \in \left[ {0,2\pi } \right]\].
Differentiating with respect to \[x\], we get
\[ \Rightarrow \dfrac{{dy}}{{dx}} = 1 + \cos x \ge 0\], \[\forall x \in {\bf{R}}\]
Again differentiating with respect to \[x\], we get
\[ \Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = - \sin x = 0{\rm{ }}\]
We know that \[\sin x = 0\] at all integers of \[\pi \].
\[ \Rightarrow x = n\pi ,n \in {\bf{Z}}\]
Therefore, \[x = n\pi \] is the point of inflection for \[f\left( x \right)\].
So, we have \[x \in \left( {0,\pi } \right)\], \[\sin x > 0\] and \[x + \sin x > x\].
Also \[x \in \left( {\pi ,2\pi } \right)\], \[\sin x < 0\]and \[x + \sin x < x\].
Using these we can draw a graph as shown below:

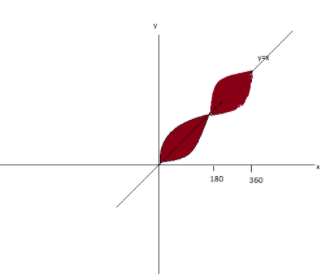
Area between two curves which intersect each other at \[\left[ {a,b} \right]\] is given by \[\int_a^c {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx + \int_c^b {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \].
Now,
 Area bounded by \[y = x + \sin x\] and its inverse \[ = \int_0^{2\pi } {\left[ {f\left( x \right) - {f^{ - 1}}\left( x \right)} \right]} dx\]
Inverse function is symmetrical with respect to \[y = x\].
Thus by using the property of symmetry, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\int_0^\pi {\left[ {f\left( x \right) - x} \right]} dx\]
Substituting the function \[f\left( x \right) = x + \sin x\], we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\int_0^\pi {\left[ {\left( {x + \sin x} \right) - x} \right]} dx\]
Subtracting the terms in the integrand, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\int_0^\pi {\sin x} dx\]
Integrating the function, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\left[ { - \cos x} \right]_0^\pi \]
Substituting the upper limit and lower limit, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\left[ { - \cos \pi - \left( { - \cos 0} \right)} \right]\]
Adding and multiplying, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\left[ { - \left( { - 1} \right) - \left( { - 1} \right)} \right]\]
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\left[ {1 + 1} \right]\]
Adding the terms, we get
\[ \Rightarrow \] Area bounded by \[y = x + \sin x\] and its inverse \[ = 4\left( 2 \right) = 8\] sq. units

Therefore, the area bounded by \[y = x + \sin x\] and its inverse between \[x = 0\] and \[x = 2\pi \] is 8 sq. units.

Note:
We need to keep in mind that, while doing integration, we should notice from the graph the curve at the bottom should be subtracted from the curve at the top. We should also know that the inflection point is a point where a function changes its sign and its direction. We should remember that the function has to be differentiated twice to find the inflection points. The limits of the integral become when both the curves are symmetrical to each other.