
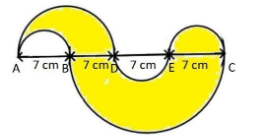
Find the area and the perimeter of the shaded portion in the adjoining figure:

Answer
587.7k+ views
Hint – In this area based question we have to find the area of the shaded region. It is clear that the shaded region can easily be obtained by reducing the two smaller semicircles and from the two larger semicircles and adding this to the area of the outer smaller semicircle. Use this concept along with a basic area formula for the area of semicircles and basic concept of perimeter of 2-D shapes to get the answer.
Complete step-by-step answer:
As we know that the area (A) of the circle is $\pi {r^2}$ (where r is the radius of the circle).
Now as we know that diameter (d) of a circle is twice the radius.
$\begin{gathered}
\Rightarrow d = 2r \\
\Rightarrow r = \dfrac{d}{2} \\
\end{gathered} $
So substitute this value in the formula of area of circle we have
$ \Rightarrow A = \pi {\left( {\dfrac{d}{2}} \right)^2} = \pi \dfrac{{{d^2}}}{4}$
Now the area of the semi-circle (${A_1}$) is half the area of the circle.
$ \Rightarrow {A_1} = \dfrac{A}{2} = \dfrac{{\pi \dfrac{{{d^2}}}{4}}}{2} = \pi \dfrac{{{d^2}}}{8}$ Sq. unit............ (1)
Now from figure the diameter of the semicircle AD is = (7 + 7) = 14 cm
Diameter of the semicircle BC = (7 + 7 + 7) = 21 cm.
Diameters of the semicircle AB, DE and EC are the same = 7 cm.
So the area of the shaded region is = area of the semicircle AD + area of the semicircle BC +area of the semicircle EC – area of the semicircle AB – area of the semicircle DE.
Now from equation (1) area of the semicircle = $\pi \dfrac{{{d^2}}}{8}$ square units.
So, the area of the shaded region is = $\pi \dfrac{{d_{AD}^2}}{8} + \pi \dfrac{{d_{BC}^2}}{8} + \pi \dfrac{{d_{EC}^2}}{8} - \pi \dfrac{{d_{AB}^2}}{8} - \pi \dfrac{{d_{DE}^2}}{8}$
Now substitute the values we have,
So, the area of the shaded region is = $\pi \dfrac{{{{\left( {14} \right)}^2}}}{8} + \pi \dfrac{{{{\left( {21} \right)}^2}}}{8} + \pi \dfrac{{{{\left( 7 \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8}$
Now simplify we have,
So, the area (A) of the shaded region is = \[\pi \dfrac{{{{\left( {14} \right)}^2}}}{8} + \pi \dfrac{{{{\left( {21} \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8}\]
$ \Rightarrow A = \dfrac{{22}}{7} \times \dfrac{{{{\left( {14} \right)}^2}}}{8} + \dfrac{{22}}{7} \times \dfrac{{{{\left( {21} \right)}^2}}}{8} - \dfrac{{22}}{7} \times \dfrac{{{{\left( 7 \right)}^2}}}{8}$, $\left[ {\therefore \pi = \dfrac{{22}}{7}} \right]$
$ \Rightarrow A = 22 \times \dfrac{{2\left( {14} \right)}}{8} + 22 \times \dfrac{{3\left( {21} \right)}}{8} - 22 \times \dfrac{7}{8}$
Now take LCM we have,
$ \Rightarrow A = \dfrac{{44\left( {14} \right) + 66\left( {21} \right) - 22\left( 7 \right)}}{8}$
$ \Rightarrow A = \dfrac{{44\left( {14} \right) + 66\left( {21} \right) - 22\left( 7 \right)}}{8} = \dfrac{{1848}}{8} = 231$ Square centimeter.
Now as we know that the perimeter of any shape is the sum of all the side length but in case of circle perimeter is same as the circumference of the circle.
As we all know that the circumference of the circle is $2\pi r$, where r is the radius of the circle.
So the perimeter/circumference of the semicircle = $\dfrac{{2\pi r}}{2} = \pi r$.
Now the radius of the circle is half of the diameter so the perimeter of the semicircle in terms of the diameter = $\dfrac{{\pi d}}{2}$ units.
So the perimeter of the given figure = perimeter of the semicircle AD + perimeter of the semicircle BC +perimeter of the semicircle EC + perimeter of the semicircle AB + perimeter of the semicircle DE.
So, the perimeter of the given figure is = $\pi \dfrac{{{d_{AD}}}}{2} + \pi \dfrac{{{d_{BC}}}}{2} + \pi \dfrac{{{d_{EC}}}}{2} + \pi \dfrac{{{d_{AB}}}}{2} + \pi \dfrac{{{d_{DE}}}}{2}$
Now substitute the values we have,
So, the perimeter (P) of the given figure is = $\pi \dfrac{{\left( {14} \right)}}{2} + \pi \dfrac{{\left( {21} \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2}$
$ \Rightarrow P = \dfrac{{22}}{7} \times \dfrac{{\left( {14} \right)}}{2} + \dfrac{{22}}{7} \times \dfrac{{\left( {21} \right)}}{2} + 3 \times \dfrac{{22}}{7} \times \dfrac{{\left( 7 \right)}}{2}$, $\left[ {\therefore \pi = \dfrac{{22}}{7}} \right]$
$ \Rightarrow P = 22 \times \dfrac{2}{2} + 22 \times \dfrac{3}{2} + 3 \times 22 \times \dfrac{1}{2}$
Now take LCM we have,
$ \Rightarrow P = \dfrac{{44 + 66 + 66}}{2}$
$ \Rightarrow P = 22 + 33 + 33 = 88$ Centimeter.
So this is the required answer.
Note – Whenever we face such types of problems the key concept is to have the good understanding of the diagrammatic representation of the figure in order to figure out the required shaded region. The good gist of the basic area formula for curves like circle always helps to get on the right track to reach the answer and also recall that the perimeter of the circle is nothing but the circumference of the circle.
Complete step-by-step answer:
As we know that the area (A) of the circle is $\pi {r^2}$ (where r is the radius of the circle).
Now as we know that diameter (d) of a circle is twice the radius.
$\begin{gathered}
\Rightarrow d = 2r \\
\Rightarrow r = \dfrac{d}{2} \\
\end{gathered} $
So substitute this value in the formula of area of circle we have
$ \Rightarrow A = \pi {\left( {\dfrac{d}{2}} \right)^2} = \pi \dfrac{{{d^2}}}{4}$
Now the area of the semi-circle (${A_1}$) is half the area of the circle.
$ \Rightarrow {A_1} = \dfrac{A}{2} = \dfrac{{\pi \dfrac{{{d^2}}}{4}}}{2} = \pi \dfrac{{{d^2}}}{8}$ Sq. unit............ (1)
Now from figure the diameter of the semicircle AD is = (7 + 7) = 14 cm
Diameter of the semicircle BC = (7 + 7 + 7) = 21 cm.
Diameters of the semicircle AB, DE and EC are the same = 7 cm.
So the area of the shaded region is = area of the semicircle AD + area of the semicircle BC +area of the semicircle EC – area of the semicircle AB – area of the semicircle DE.
Now from equation (1) area of the semicircle = $\pi \dfrac{{{d^2}}}{8}$ square units.
So, the area of the shaded region is = $\pi \dfrac{{d_{AD}^2}}{8} + \pi \dfrac{{d_{BC}^2}}{8} + \pi \dfrac{{d_{EC}^2}}{8} - \pi \dfrac{{d_{AB}^2}}{8} - \pi \dfrac{{d_{DE}^2}}{8}$
Now substitute the values we have,
So, the area of the shaded region is = $\pi \dfrac{{{{\left( {14} \right)}^2}}}{8} + \pi \dfrac{{{{\left( {21} \right)}^2}}}{8} + \pi \dfrac{{{{\left( 7 \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8}$
Now simplify we have,
So, the area (A) of the shaded region is = \[\pi \dfrac{{{{\left( {14} \right)}^2}}}{8} + \pi \dfrac{{{{\left( {21} \right)}^2}}}{8} - \pi \dfrac{{{{\left( 7 \right)}^2}}}{8}\]
$ \Rightarrow A = \dfrac{{22}}{7} \times \dfrac{{{{\left( {14} \right)}^2}}}{8} + \dfrac{{22}}{7} \times \dfrac{{{{\left( {21} \right)}^2}}}{8} - \dfrac{{22}}{7} \times \dfrac{{{{\left( 7 \right)}^2}}}{8}$, $\left[ {\therefore \pi = \dfrac{{22}}{7}} \right]$
$ \Rightarrow A = 22 \times \dfrac{{2\left( {14} \right)}}{8} + 22 \times \dfrac{{3\left( {21} \right)}}{8} - 22 \times \dfrac{7}{8}$
Now take LCM we have,
$ \Rightarrow A = \dfrac{{44\left( {14} \right) + 66\left( {21} \right) - 22\left( 7 \right)}}{8}$
$ \Rightarrow A = \dfrac{{44\left( {14} \right) + 66\left( {21} \right) - 22\left( 7 \right)}}{8} = \dfrac{{1848}}{8} = 231$ Square centimeter.
Now as we know that the perimeter of any shape is the sum of all the side length but in case of circle perimeter is same as the circumference of the circle.
As we all know that the circumference of the circle is $2\pi r$, where r is the radius of the circle.
So the perimeter/circumference of the semicircle = $\dfrac{{2\pi r}}{2} = \pi r$.
Now the radius of the circle is half of the diameter so the perimeter of the semicircle in terms of the diameter = $\dfrac{{\pi d}}{2}$ units.
So the perimeter of the given figure = perimeter of the semicircle AD + perimeter of the semicircle BC +perimeter of the semicircle EC + perimeter of the semicircle AB + perimeter of the semicircle DE.
So, the perimeter of the given figure is = $\pi \dfrac{{{d_{AD}}}}{2} + \pi \dfrac{{{d_{BC}}}}{2} + \pi \dfrac{{{d_{EC}}}}{2} + \pi \dfrac{{{d_{AB}}}}{2} + \pi \dfrac{{{d_{DE}}}}{2}$
Now substitute the values we have,
So, the perimeter (P) of the given figure is = $\pi \dfrac{{\left( {14} \right)}}{2} + \pi \dfrac{{\left( {21} \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2} + \pi \dfrac{{\left( 7 \right)}}{2}$
$ \Rightarrow P = \dfrac{{22}}{7} \times \dfrac{{\left( {14} \right)}}{2} + \dfrac{{22}}{7} \times \dfrac{{\left( {21} \right)}}{2} + 3 \times \dfrac{{22}}{7} \times \dfrac{{\left( 7 \right)}}{2}$, $\left[ {\therefore \pi = \dfrac{{22}}{7}} \right]$
$ \Rightarrow P = 22 \times \dfrac{2}{2} + 22 \times \dfrac{3}{2} + 3 \times 22 \times \dfrac{1}{2}$
Now take LCM we have,
$ \Rightarrow P = \dfrac{{44 + 66 + 66}}{2}$
$ \Rightarrow P = 22 + 33 + 33 = 88$ Centimeter.
So this is the required answer.
Note – Whenever we face such types of problems the key concept is to have the good understanding of the diagrammatic representation of the figure in order to figure out the required shaded region. The good gist of the basic area formula for curves like circle always helps to get on the right track to reach the answer and also recall that the perimeter of the circle is nothing but the circumference of the circle.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




