
Find square root of 7.1289 by long division method.
Answer
608.7k+ views
Hint: Follow the rule of division method for finding the square root of any number. Put bars from the unit place and use two digits for one bar. Now think of the largest number whose square is even to just less than the first bar digit in the number. Now subtract and bring down the quotient to the divisor, now add a new digit in quotient and divisor (in front) and repeat it to get the quotient. At last when the remainder becomes 0, quotient is the square root of it.
Complete step-by-step solution -
Division method for finding square root can be given as
(a) First place a bar over every pair of digits starting from unit digit, if the number of digits are odd then the left most single digit will also have a bar.
(b) Think of the largest number whose square is even to first less than the first bar digit. Take this number as divisor and also as quotient.
(c) Next subtract the product of the divisor and the quotient from the first bar digit and bring down the next pair of digits which have a bar to the right side of the remainder, that becomes a new dividend.
(d) Now, the new divisor is obtained by adding the first divisor and the quotient and add a digit to the right side of it that we have to choose according to the new dividend which is chosen in such a way that product of new divisor and this digit is less than or equal to the new dividend.
(e) Repeat steps (b, c, d) till the bar digit has been taken up. Now quotient is the required square root of the given number.
Now, we need to find the square root of 7.1289 by the above rules of division method. So, we can put bars to the given number from the last digit in pairs. So, we get number 7.1283 as $\overline{7}.\overline{12}\overline{89}$ (after putting bars as per the rule).
Now, we have a single digit number ‘7’ and hence we need to find any number such that the square of that number is just less than 7. So, we know
${{2}^{2}}<7<{{3}^{2}}$
Hence, divide the number $\overline{7}.\overline{12}\overline{89}$ by 2 and put quotient ‘2’ as well in the following way:
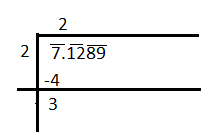
Now, add the quotient ‘2’ to the number 2 as per the steps. So, we get
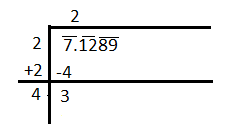
Now, put the decimal after the number 2 in the quotient and put ‘12’ adjacent to 3. So, we get
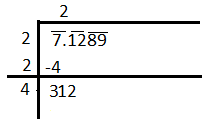
Now, as per the rules, we need to put a number in the divisor part (i.e. adjacent to 4) and the same number in the quotient as well such that multiplication of the number in the divisor and the digit in the quotient is just less than or equal to the number 312. So, we can observe that
$\begin{align}
& 46\times 6=276 \\
& 47\times 7=329 \\
\end{align}$
So, we need to put 6 to the adjacent ‘4’. So, we get
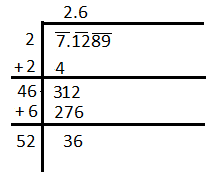
Now, in the similar way, put 89 (whole number) adjacent to 36 and divide 3689 with putting a digit adjacent to 52 and same digit to the quotient as well. So, we get

Hence, the square root of $\overline{7}.\overline{12}\overline{89}$ or 7.1289 is the quotient in the division method i.e. 2.67. Hence, 2.67 is the answer.
Note: Don’t put bars from the starting of a number in the division method. It is a general mistake done by students with this method. Always put the same digit in divisor and quotient. They should be the same for getting the square root. Bars should be only on maximum two digits and minimum on one digit.
One can verify the square root by calculating it by prime factorization method.
Complete step-by-step solution -
Division method for finding square root can be given as
(a) First place a bar over every pair of digits starting from unit digit, if the number of digits are odd then the left most single digit will also have a bar.
(b) Think of the largest number whose square is even to first less than the first bar digit. Take this number as divisor and also as quotient.
(c) Next subtract the product of the divisor and the quotient from the first bar digit and bring down the next pair of digits which have a bar to the right side of the remainder, that becomes a new dividend.
(d) Now, the new divisor is obtained by adding the first divisor and the quotient and add a digit to the right side of it that we have to choose according to the new dividend which is chosen in such a way that product of new divisor and this digit is less than or equal to the new dividend.
(e) Repeat steps (b, c, d) till the bar digit has been taken up. Now quotient is the required square root of the given number.
Now, we need to find the square root of 7.1289 by the above rules of division method. So, we can put bars to the given number from the last digit in pairs. So, we get number 7.1283 as $\overline{7}.\overline{12}\overline{89}$ (after putting bars as per the rule).
Now, we have a single digit number ‘7’ and hence we need to find any number such that the square of that number is just less than 7. So, we know
${{2}^{2}}<7<{{3}^{2}}$
Hence, divide the number $\overline{7}.\overline{12}\overline{89}$ by 2 and put quotient ‘2’ as well in the following way:
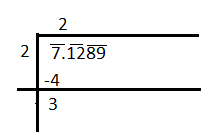
Now, add the quotient ‘2’ to the number 2 as per the steps. So, we get
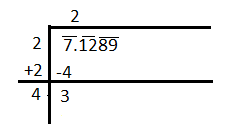
Now, put the decimal after the number 2 in the quotient and put ‘12’ adjacent to 3. So, we get
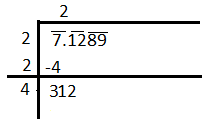
Now, as per the rules, we need to put a number in the divisor part (i.e. adjacent to 4) and the same number in the quotient as well such that multiplication of the number in the divisor and the digit in the quotient is just less than or equal to the number 312. So, we can observe that
$\begin{align}
& 46\times 6=276 \\
& 47\times 7=329 \\
\end{align}$
So, we need to put 6 to the adjacent ‘4’. So, we get
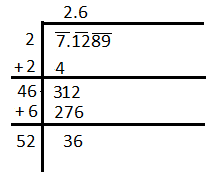
Now, in the similar way, put 89 (whole number) adjacent to 36 and divide 3689 with putting a digit adjacent to 52 and same digit to the quotient as well. So, we get

Hence, the square root of $\overline{7}.\overline{12}\overline{89}$ or 7.1289 is the quotient in the division method i.e. 2.67. Hence, 2.67 is the answer.
Note: Don’t put bars from the starting of a number in the division method. It is a general mistake done by students with this method. Always put the same digit in divisor and quotient. They should be the same for getting the square root. Bars should be only on maximum two digits and minimum on one digit.
One can verify the square root by calculating it by prime factorization method.
Recently Updated Pages
Sam invested Rs15000 at 10 per annum for one year If class 8 maths CBSE

Magesh invested 5000 at 12 pa for one year If the interest class 8 maths CBSE

Arnavs father is 49 years old He is nine years older class 8 maths CBSE

2 pipes running together can fill a cistern in 6 minutes class 8 maths CBSE

If a man were to sell his handcart for Rs720 he would class 8 maths CBSE

By using the formula find the amount and compound interest class 8 maths CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE

Application to your principal for the character ce class 8 english CBSE

Full form of STD, ISD and PCO

What are gulf countries and why they are called Gulf class 8 social science CBSE




