Question

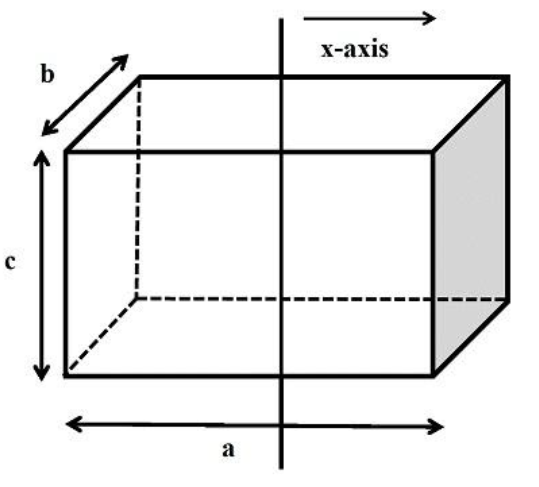
Find moment of inertia of cuboid along the axis as shown in figure.

Answer 1

Hint: In order to find the moment of inertia of the cuboid, first of all we need to find the moment of inertia for each lamina. After that we need to divide that lamina into very small rods and find its moment of inertia. Then we can find out the sum of the moment of inertia for the whole cuboid.

Complete step by step answer:
Step 1:
We will take a lamina of the cuboid with length ‘a’ and breadth ‘b’
Therefore, if we rotate it along the ‘x’ axis, we get ${I_x} + {I_y} = {I_z}$which is the moment of inertia for the lamina.
Let us assume the mass of the cuboid be M

Step 2:
Now, we know that moment of inertia of a rod with mass ‘m’ and length ‘l’ is $\dfrac{{m{l^2}}}{3}$
We need to divide the lamina in the form of small rods.
Then, moment of inertia will become $\dfrac{{{m_1}{l^2}}}{3} + \dfrac{{{m_2}{l^2}}}{3} + ............\dfrac{{{m_n}{l^2}}}{3}$$ = $$\dfrac{{{l^2}}}{3}(M)$
Similarly, we need to divide the lamina into smaller parts.

Step 3:
Now, for the lamina, we need to find the moment of inertia along ‘x’ and ‘y’ axis
Therefore, we know for a rectangular lamina, ${I_x} = \dfrac{{m{a^2}}}{{12}}$ and ${I_y} = \dfrac{{m{b^2}}}{{12}}$
Now, we can write,${I_z} = \dfrac{{m{a^2}}}{{12}} + \dfrac{{m{b^2}}}{{12}}$$ = \dfrac{{m\left( {{a^2} + {b^2}} \right)}}{{12}}$
Step four
Now Moment of inertia for the cuboid can be written as, $I = \dfrac{{{m_1}({a^2} + {b^2})}}{{12}} + \dfrac{{{m_2}({a^2} + {b^2})}}{{12}} + ......... + \dfrac{{{m_n}({a^2} + {b^2})}}{{12}}$
$I = \dfrac{{M({a^2} + {b^2})}}{{12}}$
Hence, the required moment of inertia for the cuboid is $I = \dfrac{{M({a^2} + {b^2})}}{{12}}$

Hence, the correct answer is option (B).

Note: As we know that the cuboid has some thickness along with length and breadth, so we need to find the moment of inertia along all the three axes i.e. x, y and z axis and then we need to add them. Also, we need to be clear with the formulas of moment of inertia for different dimensions and use them accordingly for different dimensions.