Question

Explain what is a Plane progressive harmonic wave ?

Answer 1

Hint: A type of wave in which all the particles perform simple harmonic motion about their mean position. The equation of plane progressive waves is determined by using the concept of simple harmonic motion. All the particles have the same amplitude in the plane progresive wave.

Complete answer:
A plane progressive harmonic wave is a wave which travels in given directions without change of its form and every particle of medium performs simple harmonic motion about their mean position with equal amplitude and time period.

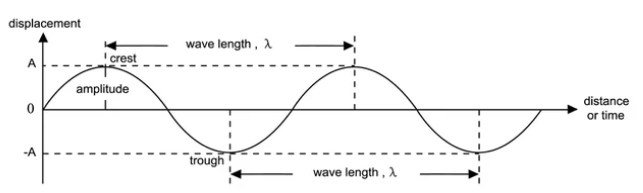
When we consider a particle at point $P$ at $x$ distance from origin $O $. The particle performs simple harmonic motion with equal amplitude and time period. The disturbance at $O$ travels and reaches point $P$ after some time. Hence the displacement of particle from equilibrium position at time $t$ is given by
$y=asin(\omega t-\varphi )$
where, $a$=amplitude, $\omega =$Angular Frequency and $\varphi =$phase difference

Phase difference depends on the path difference OP
$\varphi =\dfrac{2\pi x}{\lambda }$
where, x$=$path difference and $\lambda =$ wavelength.
$y=a\sin (\omega t-\dfrac{2\pi x}{\lambda })$
$\therefore y=a\sin (\omega t-kx)$..............$(\because k=\dfrac{\text{2}\pi }{\lambda })$
Where, $k$ is Angular wave number.

Characteristics of a Plane Progressive harmonic wave:
-When there is a disturbance in any wave then all the particles of the medium perform simple harmonic motion.
-All the particles have same amplitude
-All the particles vibrate with same frequency
-Energy is transmitted through the medium

Note:When the wave disturbance travel in positive x-axis then the equation is
$y=a\sin (\omega t-kx)$. When the wave travels in the negative x-axis then the equation is $y=a\sin (\omega t+kx)$. Somewhere the equation will be $y=a\sin (\omega t-kx+\partial)$ where the $\partial $ is the initial phase difference. In the above derivation we take the initial phase difference to be zero.