
Explain vectors with the help of examples.
Answer
518.7k+ views
Hint: Some quantities have two characteristics, a magnitude and a direction while some have only magnitude and no direction. Such quantities help us deal with multi-dimensional problems. They are represented by an arrow.
Complete answer:
A quantity which has both magnitude and direction is called a vector.A vector is defined by its magnitude that is length and its orientation that is the direction. Examples of vector quantities are velocity,displacement etc.A vector is represented by use of an arrow in a specific direction drawn to scale. Representation:$\overrightarrow{A}$
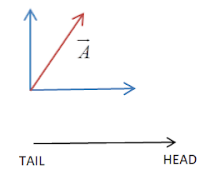
-The vector arrow has a head and a tail.
-Magnitude of a vector is shown as the length of the line segment.
-Direction is shown by the orientation of the line segment and by an arrow at one end.
Types of vectors: There are many different types of vectors:
Equal vectors: Two vectors in the same direction having equal magnitudes are called equal vectors. Example:
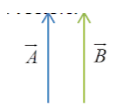
Zero vector: A vector whose magnitude is 0 is called a zero vector. It is also called a null vector. It does not have a defined direction. Example: Velocity of an object at rest is represented by a null vector.
Unit vector: As the name suggests, a vector with unit magnitude and fixed direction is called a unit vector. It is represented as \[\widehat{A}=\dfrac{\overrightarrow{A}}{\left| \overrightarrow{A} \right|}\]
Where $\widehat{A}$= Unit vector of $A$, $\overrightarrow{A}$= Vector $A$ and $\left| \overrightarrow{A} \right|$=Magnitude of vector $A$.
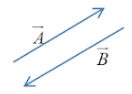
Negative vectors: Two vectors having the same magnitude but are in the opposite direction are called negative vectors. Example:
Co-initial Vectors: sets of vectors that start from one point towards the outer direction are called co-initial vectors. Example:
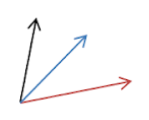
Coterminous Vectors: Set of vectors that terminate/end at one common point and point towards the common point are called coterminous vectors. Example:
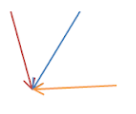
Collinear vectors: Vectors which lie on the same line or coincide with each other are called collinear vectors. Angle between the vectors must be either ${{0}^{{}^\circ }}$ or ${{180}^{{}^\circ }}$. Example:
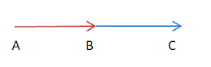
$\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear vectors.
Coplanar vectors: vectors in the same plane are called coplanar vectors. Example:

$\overrightarrow{XY}$,$\overrightarrow{YZ}$ and $\overrightarrow{XZ}$ are coplanar vectors.
Parallel vectors: Two vectors are parallel if they either point in the same direction or in the opposite directions. The magnitude need not be the same. They are of two types:
-Like parallel vectors: which point in the same direction.
Example:

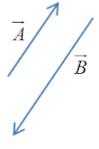
-Unlike parallel vectors: which point in the opposite direction.
Example:
Note: Quantities which require both magnitude and direction to be expressed are called vectors. Vectors can be defined in two dimensional or three dimensional space. A vector is represented by an arrow with a head and a tail.
Complete answer:
A quantity which has both magnitude and direction is called a vector.A vector is defined by its magnitude that is length and its orientation that is the direction. Examples of vector quantities are velocity,displacement etc.A vector is represented by use of an arrow in a specific direction drawn to scale. Representation:$\overrightarrow{A}$

-The vector arrow has a head and a tail.
-Magnitude of a vector is shown as the length of the line segment.
-Direction is shown by the orientation of the line segment and by an arrow at one end.
Types of vectors: There are many different types of vectors:
Equal vectors: Two vectors in the same direction having equal magnitudes are called equal vectors. Example:
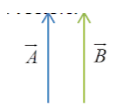
Zero vector: A vector whose magnitude is 0 is called a zero vector. It is also called a null vector. It does not have a defined direction. Example: Velocity of an object at rest is represented by a null vector.
Unit vector: As the name suggests, a vector with unit magnitude and fixed direction is called a unit vector. It is represented as \[\widehat{A}=\dfrac{\overrightarrow{A}}{\left| \overrightarrow{A} \right|}\]
Where $\widehat{A}$= Unit vector of $A$, $\overrightarrow{A}$= Vector $A$ and $\left| \overrightarrow{A} \right|$=Magnitude of vector $A$.
Negative vectors: Two vectors having the same magnitude but are in the opposite direction are called negative vectors. Example:

Co-initial Vectors: sets of vectors that start from one point towards the outer direction are called co-initial vectors. Example:

Coterminous Vectors: Set of vectors that terminate/end at one common point and point towards the common point are called coterminous vectors. Example:

Collinear vectors: Vectors which lie on the same line or coincide with each other are called collinear vectors. Angle between the vectors must be either ${{0}^{{}^\circ }}$ or ${{180}^{{}^\circ }}$. Example:

$\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear vectors.
Coplanar vectors: vectors in the same plane are called coplanar vectors. Example:

$\overrightarrow{XY}$,$\overrightarrow{YZ}$ and $\overrightarrow{XZ}$ are coplanar vectors.
Parallel vectors: Two vectors are parallel if they either point in the same direction or in the opposite directions. The magnitude need not be the same. They are of two types:
-Like parallel vectors: which point in the same direction.
Example:

-Unlike parallel vectors: which point in the opposite direction.
Example:

Note: Quantities which require both magnitude and direction to be expressed are called vectors. Vectors can be defined in two dimensional or three dimensional space. A vector is represented by an arrow with a head and a tail.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




