Question

Evaluate the following: $\left( {{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ \right)\left( \cos e{{c}^{2}}45{}^\circ {{\sec }^{2}}30{}^\circ \right)$ .

Answer 1

Hint: Try to simplify the expression given in the question using the values of $\cot 45{}^\circ $ , $\sin 30{}^\circ $ and other required values. Just put the values and solve the expression to get the answer.

Complete step-by-step answer:


Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.

First, let us start with the graph of sinx.

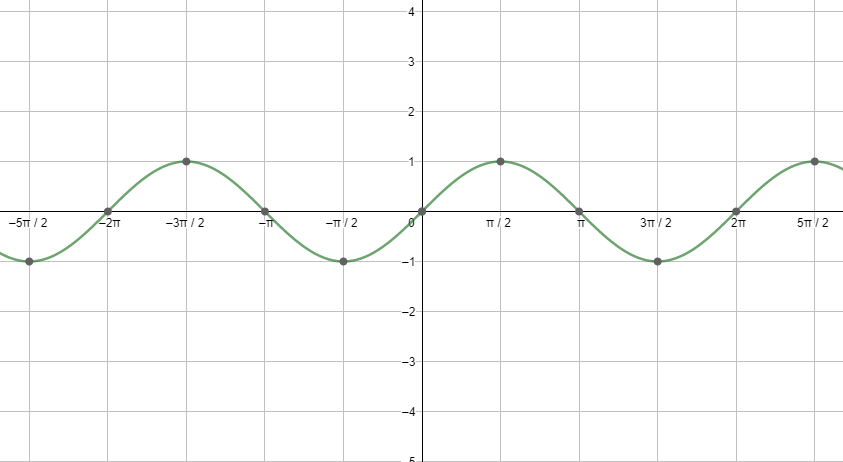
Next, let us see the graph of cosx.

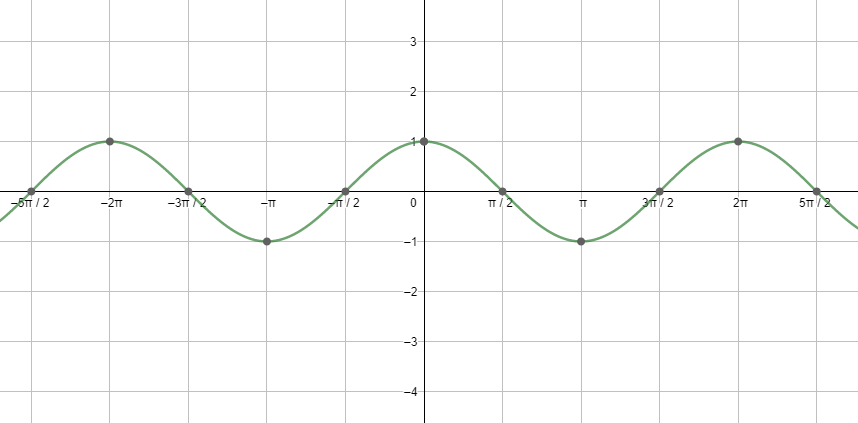
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ $

Now to start with the solution to the above question, we will try to simplify the expression given in the question by putting the values $\cot 45{}^\circ =1$ and $\operatorname{cosec}45{}^\circ =\sqrt{2}$ . On doing so, we get

$\left( {{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ \right)\left( \cos e{{c}^{2}}45{}^\circ {{\sec }^{2}}30{}^\circ \right)$

$=\left( {{\sin }^{2}}30{}^\circ +4\times 1-{{\sec }^{2}}60{}^\circ \right)\left( {{\left( \sqrt{2} \right)}^{2}}{{\sec }^{2}}30{}^\circ \right)$

$=\left( {{\sin }^{2}}30{}^\circ +4-{{\sec }^{2}}60{}^\circ \right)\left( 2{{\sec }^{2}}30{}^\circ \right)$

Now we also know that $\sin 30{}^\circ =\dfrac{1}{2}$ , $\sec 30{}^\circ =\dfrac{2}{\sqrt{3}}$ and $\sec 60{}^\circ =2$ . So, if we put these values in our expression, we get

$=\left( {{\left( \dfrac{1}{2} \right)}^{2}}+4-{{2}^{2}} \right)\left( 2{{\left( \dfrac{2}{\sqrt{3}} \right)}^{2}} \right)$

$=\dfrac{1}{4}\left( 2\times \dfrac{4}{3} \right)$

$=\dfrac{2}{3}$

Therefore, we can say that the value of $\left( {{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ \right)\left( \cos e{{c}^{2}}45{}^\circ {{\sec }^{2}}30{}^\circ \right)$ is equal to $\dfrac{2}{3}$ .


Note: Be careful about the calculation and the signs of the formulas you use as the signs in the formulas are very confusing and are very important for solving the problems. Also, it would help if you remember the properties related to complementary angles and trigonometric ratios.