Question

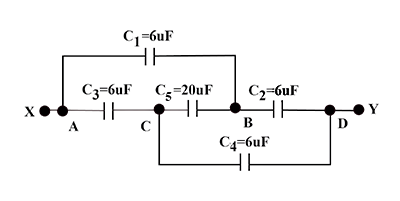
What is the effective capacitance between points X and Y?

${\text{A}}{\text{. 24}}\mu F$
${\text{B}}{\text{. 18}}\mu F$
${\text{C}}{\text{. 12}}\mu F$
${\text{D}}{\text{. 6}}\mu F$

Answer 1

- Hint – The given circuit is a Wheatstone bridge circuit and here $\dfrac{{{C_1}}}{{{C_3}}} = \dfrac{{{C_2}}}{{{C_4}}}$ . Thus, no charge flows through the capacitor ${C_5} = 20\mu F$ . Use this to solve the question.
Formula used - $\dfrac{{{C_1}}}{{{C_3}}} = \dfrac{{{C_2}}}{{{C_4}}}$ , ${C_{13}} = \dfrac{{{C_1} \times {C_3}}}{{{C_1} + {C_3}}}$ , ${C_{24}} = \dfrac{{{C_2} \times {C_4}}}{{{C_2} + {C_4}}}$ , ${C_{XY}} = {C_{13}} + {C_{24}}$

Complete step-by-step solution -

The circuit given in the question is a Wheatstone bridge circuit and here $\dfrac{{{C_1}}}{{{C_3}}} = \dfrac{{{C_2}}}{{{C_4}}}$ . Also, no charge flows through the capacitor ${C_5} = 20\mu F$ .
Drawing the equivalent circuit-

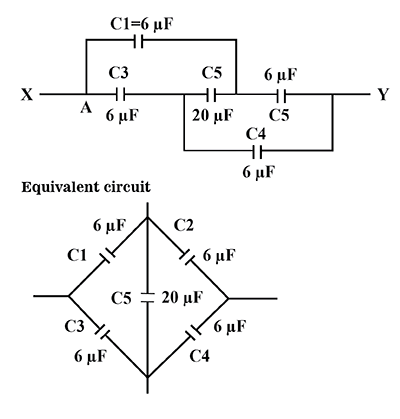
Now, we can see that C1 and C3 are in series, so the equivalent capacitance will be-
${C_{13}} = \dfrac{{{C_1} \times {C_3}}}{{{C_1} + {C_3}}}$
Putting the values of ${C_1} = 6\mu F,{C_3} = 6\mu F$ , we get-
${C_{13}} = \dfrac{{6 \times 6}}{{6 + 6}} = 3\mu F$
Also, C2 and C4 are in series, so the equivalent capacitance will be-
${C_{24}} = \dfrac{{{C_2} \times {C_4}}}{{{C_2} + {C_4}}}$
Putting the values of ${C_2} = 6\mu F,{C_4} = 6\mu F$ , we get-
${C_{24}} = \dfrac{{6 \times 6}}{{6 + 6}} = 3\mu F$
Now, ${C_{13}}$ and ${C_{24}}$ are in parallel, so now the equivalent of this combination will give us the capacitance between the points X and Y.
So, finding the value of the capacitance between X and Y.
${C_{XY}} = {C_{13}} + {C_{24}}$
putting the values, we get-
${C_{XY}} = 3 + 3 = 6\mu F$
Therefore, the effective capacitance between points X and Y is $6\mu F$ .
Hence, the correct option is D.

Note- Whenever solving such types of questions, first draw the equivalent circuit which makes it easier to solve. Also, as mentioned in the solution, the given circuit is a Wheatstone bridge circuit, so as we know, a Wheatstone bridge is an electrical circuit used to measure an unknown capacitance by balancing two legs of a bridge circuit, one leg of which includes the unknown. So, using this concept we have found out the capacitance between the given points.