Question

E is any point on median AD of triangle ABC. Show that $ ar\left( {\Delta ABE} \right) = ar\left( {\Delta ACE} \right) $ .
In a triangle ABC, E is the midpoint of median AD. Show that $ ar\left( {\Delta BED} \right) = \dfrac{1}{4}.ar\left( {\Delta ABC} \right) $ .

Answer 1

Hint: To prove required results we use the median concept of triangle as we know that every median of triangle divides triangle in two equal parts or we can say in two equal areas. Using this fact we proceed to derive required proof.

Complete step-by-step answer:
In triangle ABC, it is given that AD is median from A to BC.
Therefore D is the midpoint of BC.
 

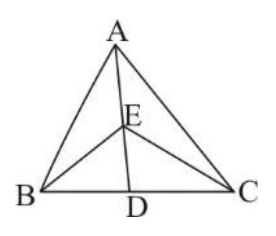
And we know that the median of a triangle divides the triangle in two equal areas.
Therefore,
 $ ar(\Delta ABD) = ar\left( {\Delta ACD} \right) $ …………………… (i)
Also, it is given that E is a midpoint on median AD.
So, BE will be a median for $ \Delta $ BAD
Therefore, $ ar(\Delta BED) = ar\left( {\Delta BEA} \right)................(ii) $
From figure we see that $ ar(\Delta ABD) = ar(\Delta BEA) + ar(\Delta BDE) $
Using (ii) in above equation we have
 $
  ar\left( {\Delta ABD} \right) = ar\left( {\Delta BDE} \right) + ar\left( {\Delta BDE} \right) \\
  ar\left( {\Delta ABD} \right) = 2.ar\left( {\Delta BDE} \right)........(iii) \\
  $ $ $
Similarly, CE is median for triangle CAD
Therefore, $ ar\left( {\Delta CEA} \right) = ar\left( {\Delta CED} \right) $
From figure we see that
  $
  ar\left( {\Delta ACD} \right) = ar\left( {CEA} \right) + ar\left( {\Delta CED} \right) \\
  ar\left( {\Delta ACD} \right) = 2.ar\left( {\Delta CED} \right)......................(iv) \\
  $

Using, (iii) and (iv) in (i) we have
 $
  2.ar\left( {\Delta BED} \right) = 2.ar\left( {\Delta CED} \right) \\
   \Rightarrow ar\left( {\Delta BED} \right) = ar\left( {\Delta CED} \right).................(v) \\
  $
Now, on subtracting (v) from (i) we have
 $
  ar\left( {\Delta ABD} \right) - ar\left( {\Delta BED} \right) = ar\left( {\Delta ACD} \right) - ar\left( {\Delta CDE} \right) \\
   \Rightarrow ar\left( {\Delta ABE} \right) = ar\left( {\Delta ACE} \right) \\
  $
Hence, from above we see that $ ar\left( {\Delta ABE} \right) = ar\left( {\Delta ACE} \right) $ . Which requires proof of the first part.

Also, from above we see that triangle ABC is divided into four equal sub parts.
Therefore,
 $ ar\left( {\Delta ABC} \right) = ar\left( {\Delta ABE} \right) + ar\left( {\Delta BDE} \right) + ar\left( {\Delta CED} \right) + ar\left( {\Delta CAE} \right) $
But as proved above we have $ ar\left( {\Delta ABE} \right) = ar\left( {\Delta BDE} \right) = ar\left( {\Delta CED} \right) = ar\left( {\Delta CAE} \right) $

Therefore, using it in above equation we have
\[
  ar\left( {\Delta ABC} \right) = 4.ar\left( {\Delta BDE} \right) \\
   \Rightarrow ar\left( {\Delta BDE} \right) = \dfrac{1}{4}.ar\left( {\Delta ABC} \right) \\
 \]
Which is the required proof of the second part.
Hence, from above we see that $ ar(\Delta ABE) = ar(\Delta AEC) $ and \[ar\left( {\Delta BDE} \right) = \dfrac{1}{4}.ar\left( {\Delta ABC} \right)\]

Note: In triangle we see that median divides the triangle in two equal parts or we can say that median divides triangle in two equal areas. Also, a triangle formed after the median also has another median then that median will also divide that triangle in two equal parts. Hence, from above we see that for every triangle whether it is a small or big median always divide it in two equal areas.