Question

Draw the line segment ($\overline {{\text{AB}}}$) of length 7.3 cm and find its axis of symmetry.

Answer 1

Hint: Here, we will proceed by drawing the line segment AB of length 7.3 cm with the help of the scale and then using the compass, follow the basic steps of construction of the axis of symmetry mentioned below.

Complete step-by-step answer:
The following steps of construction are given under:
Step1- Take a scale and draw a line segment of length 7.3 cm. Mark the end points of this line segment as A and B. This is the required $\overline {{\text{AB}}} $ of length 7.3 cm.

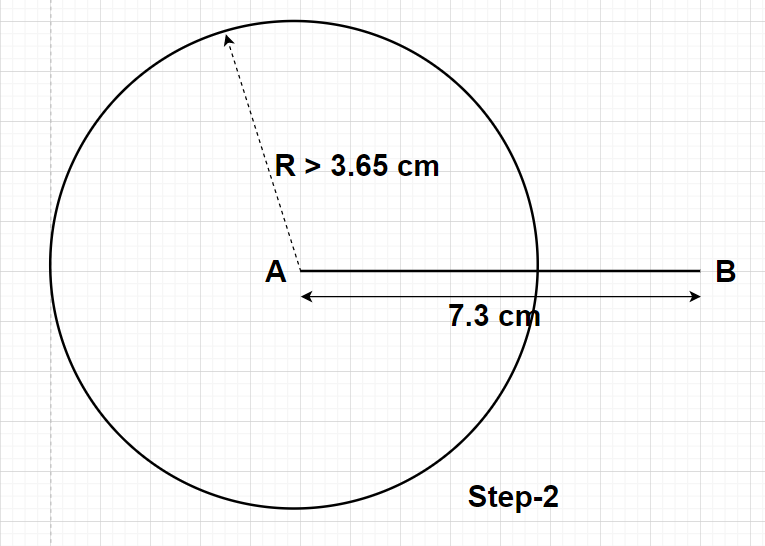
Step2- Now, take a compass and open the ends of the compass more than half of the length of the line segment AB (i.e., more than $\dfrac{{7.3}}{2}{\text{ cm}} = 3.65{\text{ cm}}$). By taking the centre as point A, draw a circle using this compass. The radius of the circle obtained will be more than half of the length of the line segment AB (i.e., the radius of the circle with a centre at A should be more than 3.65 cm).

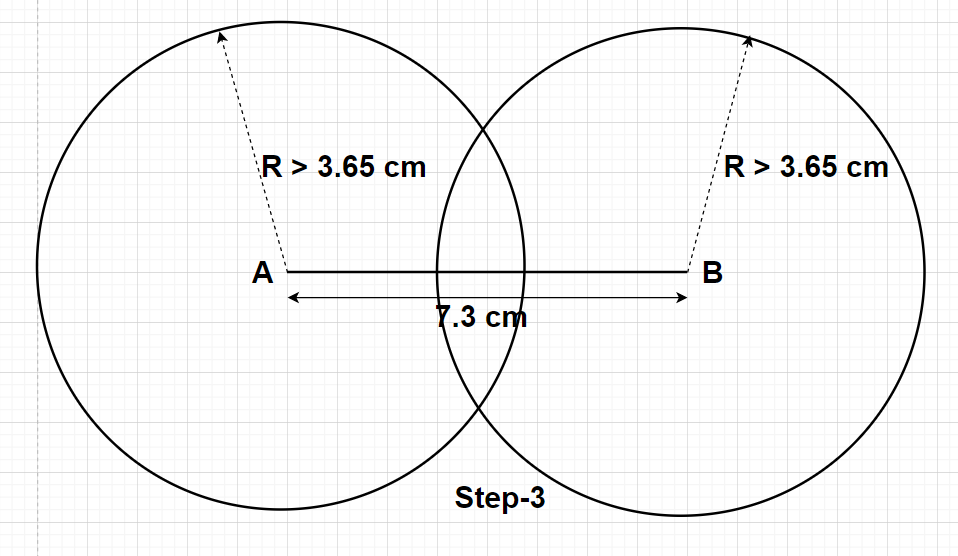
Step3- With the same radius as before or with the same distance between the ends of the compass as before, draw another circle by taking point B as the centre. The radius of this circle whose centre lies at the point B is more than half of the length of the line segment AB (i.e., the radius of the circle with centre at B will be more than 3.65 cm).

Step4- Name the points where these two circles will be intersecting as points C and D. Join these points C and D by a dotted line with the help of the scale. This CD is the required axis of symmetry of the line segment $\overline {{\text{AB}}} $ having a length of 7.3 cm.

Note: In this particular problem, the radius of the circles drawn will be equal to the distance between the ends of the compass. Here, that radius needs to be more than half of the length of the line segment whose axis of symmetry is required. There is no need to measure it with the help of the scale whereas this can be done by simple estimation.