Question

Draw the graphs of the equations:
$\begin{align}
  & 5x-y=5 \\
 & 3x-y=3 \\
\end{align}$
Determine the coordinates of the triangle formed by the lines representing the above equations and the y-axis.

Answer 1

Hint: Here, first we have to find the two points to draw the graph of the system of equations. While choosing the points, first take $x=0$ and then find y. Similarly, for $y=0$, find the value of x. With these points we can draw the graph of the system of equations and y-axis. Here, the region bounded by the equations and y-axis will be a triangle. Now, from the graph we can find the coordinates of the triangle formed by the lines representing the equations and the y-axis.

Complete step-by-step answer:

Here, we are given with the equations:
$\begin{align}
  & 5x-y=5 \\
 & 3x-y=3 \\
\end{align}$
Now, we have to determine the coordinates of the triangle formed by the lines representing the above equations and the y-axis.
 First consider the equation:
$5x-y=5$
Now, we have to draw the line corresponding to the given equation. For that consider two points.
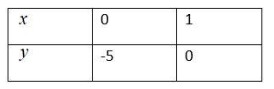
When $x=0$ we have:
$\begin{align}
  & 5\times 0-y=5 \\
 & \Rightarrow -y=5 \\
\end{align}$
Next, by cross multiplication,
$\begin{align}
  & \Rightarrow y=\dfrac{5}{-1} \\
 & \Rightarrow y=-5 \\
\end{align}$
Now, consider the equation $5x-y=5$ when $y=0$,
$\begin{align}
  & \Rightarrow 5x-0=5 \\
 & \Rightarrow 5x=5 \\
\end{align}$
In the next step, by cross multiplication,
$\begin{align}
  & \Rightarrow x=\dfrac{5}{5} \\
 & \Rightarrow x=1 \\
\end{align}$
So, we will get the table as follows:

Next, consider the equation:
$3x-y=3$
Now, we have to find two points to draw the graph of the equation.
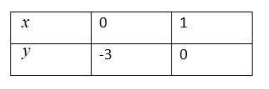
For that take when $x=0$, our equation,
$\begin{align}
  & \Rightarrow 3\times 0-y=3 \\
 & \Rightarrow 0-y=3 \\
 & \Rightarrow -y=3 \\
\end{align}$
Now, by cross multiplication,
$\begin{align}
  & \Rightarrow y=\dfrac{3}{-1} \\
 & \Rightarrow y=-3 \\
\end{align}$
Now, for $y=0$ we will obtain:
$\begin{align}
  & 3x-0=3 \\
 & \Rightarrow 3x=3 \\
\end{align}$
Hence, by cross multiplication,
$\begin{align}
  & \Rightarrow x=\dfrac{3}{3} \\
 & \Rightarrow x=1 \\
\end{align}$
Therefore, we will get the table as follows:

Now, we have to draw the graph of the given system of equations using the tables provided.

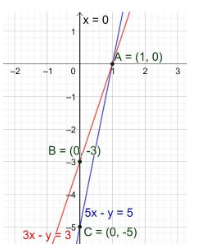
From the graph, we can say that the region bounded by the system of equations and the y-axis is a triangle $\Delta ABC$.
Hence, the coordinates of $\Delta ABC$ are A (1, 0), B (0, -3) and C (0, -5).

Note: Here, we have the graphical representation of two variables. A graph of linear equations $Ax+By=C$ is a line. Every point on the line is a solution of the equation. And also we have every solution of this equation is a point on this line. Here, also we have two linear equations and every point we mark on the line will be its solution.