
Draw the graph of the equation: $2x - 3y = 5$ .
From your graph find
I.The value of y when $x = 4$
II.The value of $x$ when $y = 3$
Answer
510k+ views
Hint: In this question we have been given a linear equation and we have to draw the graph. So we will first assume any random value of $x$ , so that we get the value of $y$ . After this we have the value of both the axis and then we put the value in the graph and then draw it. We should keep in mind that the graph of a linear equation will always be a straight line.
Complete step-by-step answer:
Here we have the equation
$2x - 3y = 5$
We can also wrote the equation as
$3y = 2x - 5$
Now we will isolate the term $y$, so it gives
$y = \dfrac{{2x - 5}}{3}$
Let us take the value of
$x = 4$ .
By substituting this in the equation, we can write
$y = \dfrac{{2(4) - 5}}{3}$
On simplifying we have
$y = \dfrac{{8 - 5}}{3}$
It gives:
$y = \dfrac{3}{3} = 1$
Now, let us take another value i.e.
$x = - 2$
By substituting this value in the equation, we have:
$y = \dfrac{{2( - 2) - 5}}{3}$
On further solving
$y = \dfrac{{ - 4 - 5}}{3}$
It gives us
$y = \dfrac{{ - 9}}{3} = - 3$
So we can now write the values:
We will now put these values in the graph:
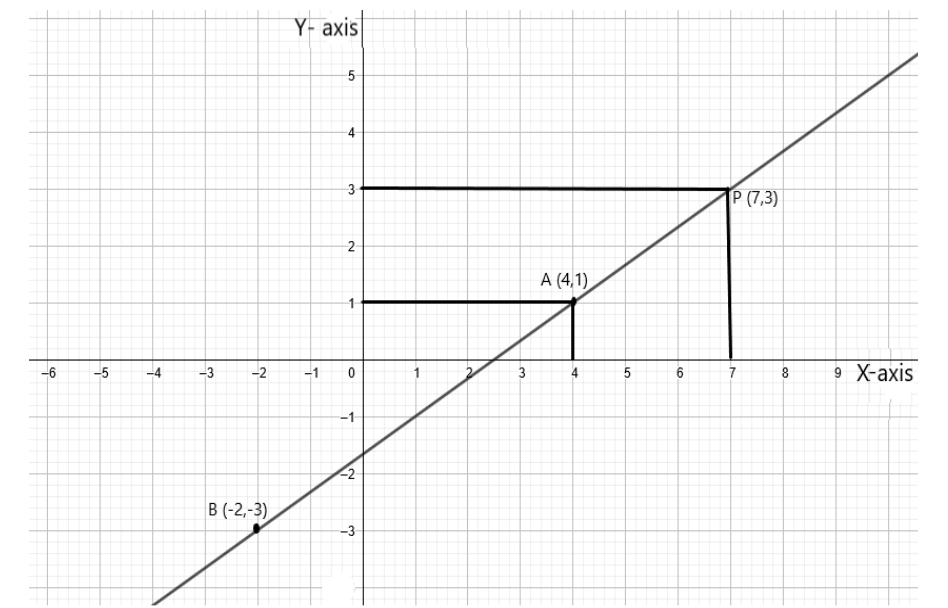
From the above graph we have the coordinates, $A(4,1)$ and $B( - 2, - 3)$ .
Based on the above graph we can also see that if we consider
$x = 4$ , then we know that the line joining the two points and a point on the Y- axis will give the value of $y$ .
Therefore we have when $x = 4$ , then the value is
$y = 1$
It gives us the same coordinate as above i.e.
$A(4,1)$
Again in the second case if we consider
$y = 3$ , then the line joining the two points and a point on the X- axis gives the value of $x$
Therefore when we have
$y = 3$ , the value on the X- axis is $x = 7$ .
Hence in the graph we have $P(7,3)$ .
Note: We should note that the standard form a linear equation is
$ax + b = 0$ . This is the example of a linear equation in one variable. If we have a linear equation in two variables, then it will be of the form $ax + by = c$ . Here $x,y$ are variables and $a,b,c$ are constants. We should know that linear equations are equations of degree $1$ .
Complete step-by-step answer:
Here we have the equation
$2x - 3y = 5$
We can also wrote the equation as
$3y = 2x - 5$
Now we will isolate the term $y$, so it gives
$y = \dfrac{{2x - 5}}{3}$
Let us take the value of
$x = 4$ .
By substituting this in the equation, we can write
$y = \dfrac{{2(4) - 5}}{3}$
On simplifying we have
$y = \dfrac{{8 - 5}}{3}$
It gives:
$y = \dfrac{3}{3} = 1$
Now, let us take another value i.e.
$x = - 2$
By substituting this value in the equation, we have:
$y = \dfrac{{2( - 2) - 5}}{3}$
On further solving
$y = \dfrac{{ - 4 - 5}}{3}$
It gives us
$y = \dfrac{{ - 9}}{3} = - 3$
So we can now write the values:
| $x$ | $4$ | $ - 2$ |
| $y$ | $1$ | $ - 3$ |
We will now put these values in the graph:

From the above graph we have the coordinates, $A(4,1)$ and $B( - 2, - 3)$ .
Based on the above graph we can also see that if we consider
$x = 4$ , then we know that the line joining the two points and a point on the Y- axis will give the value of $y$ .
Therefore we have when $x = 4$ , then the value is
$y = 1$
It gives us the same coordinate as above i.e.
$A(4,1)$
Again in the second case if we consider
$y = 3$ , then the line joining the two points and a point on the X- axis gives the value of $x$
Therefore when we have
$y = 3$ , the value on the X- axis is $x = 7$ .
Hence in the graph we have $P(7,3)$ .
Note: We should note that the standard form a linear equation is
$ax + b = 0$ . This is the example of a linear equation in one variable. If we have a linear equation in two variables, then it will be of the form $ax + by = c$ . Here $x,y$ are variables and $a,b,c$ are constants. We should know that linear equations are equations of degree $1$ .
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What are gulf countries and why they are called Gulf class 8 social science CBSE

Name the states through which the Tropic of Cancer class 8 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Who created the image of Bharat Mata for the first class 8 social science CBSE





