Question

Draw an obtuse angle. Then bisect this angle and measure the angles so obtained.

Answer 1

Hint: First draw an angle ABC where $\angle ABC=120{}^\circ $. Next construct its bisector. Draw an arc from point P as centre by setting radius more than half of PQ. Draw another arc with Q as centre and radius same as before which cuts the previous arc at R. Join RB. RB is the angle bisector and we will get $\angle ABR=\angle RBC=60{}^\circ $.

Complete step by step answer:
In this question, we need to draw an obtuse angle. Then bisect this angle and measure the
angles so obtained.
Let us first start by defining what an obtuse angle actually is.
An obtuse angle is a type of angle that is always larger than $90{}^\circ $ but less than $180{}^\circ $. In other words, it lies between a right angle and a straight angle.
Now, we will construct an obtuse angle and its bisector by the following steps:

The figure below shows the construction of obtuse angle:

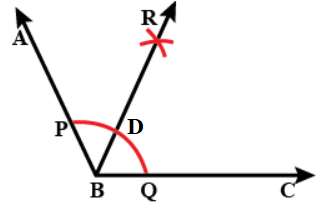
Step 1: Draw an obtuse angle. We will draw $\angle ABC=120{}^\circ $ for this question. Here B is the vertex of the angle and AB and BC are the rays of the angle.
Step 2: Draw a ray BC.
Step 3: Taking B as centre and any radius , cut an arc cutting BC at Q.
Step 4: Now, taking Q as centre and radius same as in the previous step, draw an arc intersecting the previously drawn arc at point D.
Step 5: With D as centre as radius same as before, draw an arc cutting the first arc at P.
Step 6: Join BP and extend it to A. So, $\angle ABC=120{}^\circ $.
Step 7: Draw an arc from point P as centre by setting radius more than half of PQ.
Step 8: Draw an arc from point Q as centre with radius same as in step 3, and cut the previous arc at R.
Step 9: Join BR.
Therefore, $\angle ABR=\angle RBC=60{}^\circ $

Note: In this question, it is important to note that in step 7, it is very important to keep the radius more than half of PQ and keep the radius the same for the next step. If the radius is less than half, then the new arcs will not intersect, and we will not get the point R. Also, note that the bisector of ABC will pass through the point D constructed earlier. In this way you can check whether your construction is correct or not.