Question

Draw an equilateral triangle of side 7.5 cm and locate the centroid.

Answer 1

Hint: An equilateral triangle is a triangle in which all three sides are equal and all three internal angles are also congruent to each other and are each 60°. The centroid is a point of concurrency of the median of the triangle.

Complete step by step answer:

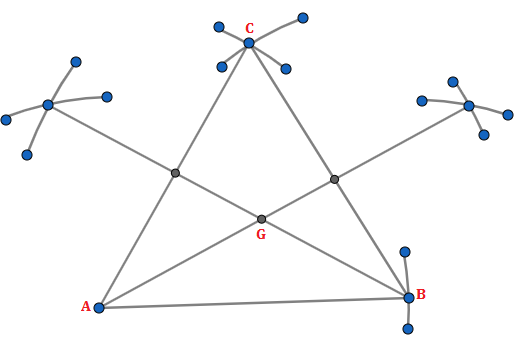
To draw an equilateral triangle and locate the centroid by using the following steps:
- Pick a point A that will be one vertex of the desired equilateral triangle.
- The compass is set to the length 7.5 cm.
- Place the compass on the point on A and make two arcs.
- Now one of the arcs, mark a point B that will be a second vertex of the triangle.
- Place the compasses on the point B and draw an arc that crosses the other arc, mark a point C that will be a third vertex of the triangle.
- Using the straightedge, draw three lines linking the points A, B and C and hence the triangle ABC is an equilateral triangle.
- Construct the perpendicular bisectors of two sides AC and BC to find the midpoints D and E of AC and BC respectively
- Draw the medians AE and BD and let them meet at G and the point G is the centroid of the given triangle ABC.

Note: Alternatively, to draw an equilateral triangle without a compass. Rotate the ruler until the mark representing the length of the base line touches the perpendicular bisector. If it cannot touch, extend the bisector. Draw the line, and then repeat this process to draw the third line. You now have a triangle with three congruent sides and three congruent angles, or an equilateral triangle.