Question

Draw a triangle $ABC$ and $AD$ as it’s median.

Answer 1

Hint: edian is nothing but a line segment from one vertex of a triangle to the opposite side’s midpoint. Hence find the midpoint and draw a line to the corresponding vertex.
 Initially draw a triangle with vertices $A,B,C$. In the triangle the sum of the angles made by the sides of the triangle should and will be ${360^ \circ }$. After drawing the triangle find the midpoint of the opposite side of $A$ i.e., $BC$. And name it as $D$. Then draw a line passing through both the vertices $A,D$ and name the line as $AD$. And finally the line $AD$ is the median.

Complete step by step solution:
Steps of construction:
Step 1: Draw a line segment $BC$ .
Step 2: Next consider any random length and construct the triangle ABC.

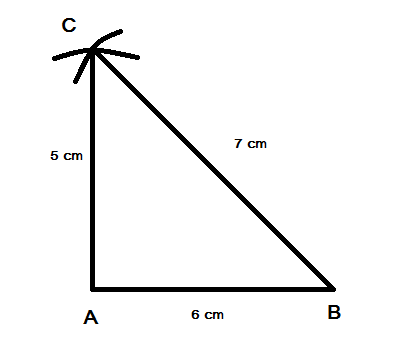
Step 3: Next, find out the longest length side and consider it as base to draw the median which is BC here.
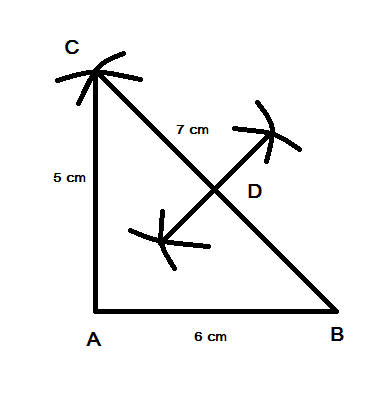
Step 4: Then perform perpendicular bisector to the base and the join the arcs
Step 5: The point where the line joining arc bisects the base is the mid point consider it as point D.

Step 6: Then connect A and D, which forms the median AD, which is required.
$\therefore \vartriangle ABC$ is the required triangle. With $AD$ as it’s median.

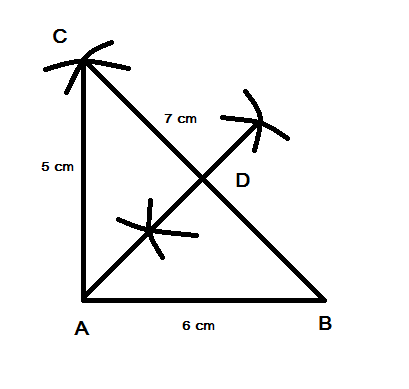
Note: While making the arcs make sure you have placed the compass correctly on the required vertices for getting the mid-point and also the median. In the triangle the sum of the angles made by the sides of the triangle should and will be ${360^ \circ }$. Median is nothing but a line segment from the vertex of a triangle to the opposite side’s midpoint. Hence find the midpoint and draw a line to the corresponding vertex. Therefore the midpoint is necessary for the median.