Question

Draw a rough sketch of the curve \[{y^2} = 4x\] and find the area of the region enclosed by the curve and the line \[y = x\] .

Answer 1

Hint: We know that \[{y^2} = 4x\] is the right handed parabola with vertex at origin and axis of the parabola is x-axis. We also know that \[y = x\] is a straight line passing through origin. We have integration formula \[\int {{x^n}.dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} \] . Using the given curve and line we can find the limits of an integration.

Complete step-by-step answer:
The required area is the shaded region. To find the area of the shaded region we find the area of the curve enclosed by parabola and area enclosed by the straight line. Taking the difference we get the required answer.
Now given, the curve \[{y^2} = 4x\] .
But we have, \[y = x\] .
Substituting in the given curve we have,
 \[ \Rightarrow {x^2} = 4x\]
 \[ \Rightarrow {x^2} - 4x = 0\]
Taking ‘x’ as common,
 \[ \Rightarrow x(x - 4) = 0\]
Using zero product property
 \[ \Rightarrow x = 0\] and \[x - 4 = 0\]
 \[ \Rightarrow x = 0\] and \[x = 4\] .
Also we have \[y = x\] then \[y = 0\] and \[y = 4\] .
Therefore points of intersection are (0, 0) and (4, 4).
Hence the limit is from 0 to 4.
Let’s look at the rough sketch of the given problem.

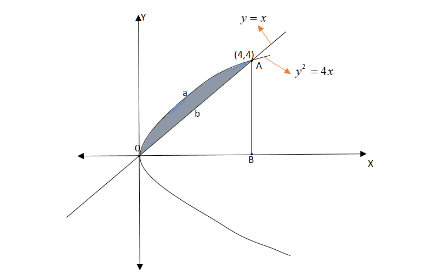
Now the area enclosed by parabola \[(BAaOB) \Rightarrow \int\limits_0^4 {\sqrt {4x} .dx} \]
 \[ \Rightarrow 2\int\limits_0^4 {\sqrt x .dx} \]
Applying integration for ‘x’,
 \[ \Rightarrow 2\left[ {\dfrac{{{x^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right] _0^4\]
Taking constant out side,
 \[ \Rightarrow 2 \times \dfrac{2}{3}\left( {{x^{\dfrac{3}{2}}}} \right)_0^4\]
Applying lower and upper limits,
 \[ \Rightarrow 2 \times \dfrac{2}{3}\left( {{4^{\dfrac{3}{2}}} - {0^{\dfrac{3}{2}}}} \right)\]
 \[ \Rightarrow 2 \times \dfrac{2}{3}\left( {{{64}^{\dfrac{1}{2}}} - 0} \right)\]
 \[ \Rightarrow 2 \times \dfrac{2}{3} \times 8\]
 \[ \Rightarrow \dfrac{{32}}{3}\] Sq. Units.
Now the area enclosed by straight line \[(BAbOB) \Rightarrow \int\limits_0^4 {x.dx} \]
 \[ \Rightarrow \left( {\dfrac{{{x^2}}}{2}} \right)_0^4\]
 \[ \Rightarrow \dfrac{1}{2}\left( {{4^2} - {0^2}} \right)\]
 \[ \Rightarrow \dfrac{1}{2} \times 16\]
 \[ \Rightarrow 8\] Sq. Units.
Now the required area = area enclosed by parabola (‘BAaOB’) – area enclosed by straight line (‘BAbOB’)
That is \[ = \dfrac{{32}}{3} - 8\]
 \[ \Rightarrow \dfrac{{32 - 24}}{3}\]
 \[ \Rightarrow \dfrac{8}{3}\] Sq. Units.
So, the correct answer is “ \[ \dfrac{8}{3}\] Sq. Units”.

Note: Know all the four types of parabola and its diagram (right handed parabola, left handed parabola, upward parabola and downward parabola). Without it we cannot solve this. Careful in the calculation part. We also know that area is always in square units. In the above we chose ‘a’ and ‘b’ path for reference.