Question

Draw a phasor diagram to represent the current and supply voltage appropriately as phasors. State the phase difference between the two quantities.

Answer 1

Hint: To draw the phasor diagram, we have to find the phase difference first. Use the formula for alternating voltage and alternating current. For voltage, at $t=\dfrac { T }{ 4 }$, $V ={V}+{0}$, substitute this value in the formula for alternating voltage and find the frequency. Similarly for current, At $t=\dfrac { T }{ 8 }$, $I ={I}_{0}$, substitute the value in alternating current formula. Now, substitute the value of obtained frequency in the formula for alternating current. Solve the obtained equation and find the phase difference.

Formula used:
$V={ V }_{ 0 }\sin { \left( \omega t \right) }$
$I= { I }_{ 0 }\sin { \left( \omega t+\phi \right) }$

Complete answer:
Let the phase difference be $\phi$.
From the figure given, we can infer that the voltage is lagging the current by a phase difference $\phi$.
Alternating voltage is given by,
$V={ V }_{ 0 }\sin { \left( \omega t \right) }$ …(1)
Alternating current is given by,
$I= { I }_{ 0 }\sin { \left( \omega t+\phi \right) }$ …(2)
At $t=\dfrac { T }{ 4 }$, $V ={V}_{0}$
Substituting this value in the equation. (1) we get,
$ V=V\sin { \left( \dfrac { \omega T }{ 4 } \right) }$
$\Rightarrow 1=\sin { \left( \dfrac { \omega T }{ 4 } \right) }$
$\Rightarrow \dfrac { \omega T }{ 4 } =\quad \dfrac { \pi }{ 2 }$
$\Rightarrow \omega =\cfrac { 2\pi }{ T }$ …(3)
Similarly, at $t=\dfrac { T }{ 8 }$, $I ={I}_{0}$
Substituting this value in the equation. (2) we get,
$I=I\sin { \left( \omega t+\phi \right) }$
$\Rightarrow 1=\sin { \left( \dfrac { \omega T }{ 8 } + \phi \right) }$ …(2)
Substituting equation. (3) in equation. (4) we get,
$\sin { \left( \dfrac { 2\pi }{ T } \times \dfrac { T }{ 8 } + \phi \right) } =\quad 1$
$\Rightarrow \sin { \left( \cfrac { \pi }{ 4 } +\phi \right) } =\quad 1$
$\Rightarrow \cfrac { \pi }{ 4 } +\phi =\cfrac { \pi }{ 2 }$
$\Rightarrow \phi =\cfrac { \pi }{ 2 }$
$\Rightarrow \phi=45°$
So, the corresponding phasor diagram can be drawn as given below,

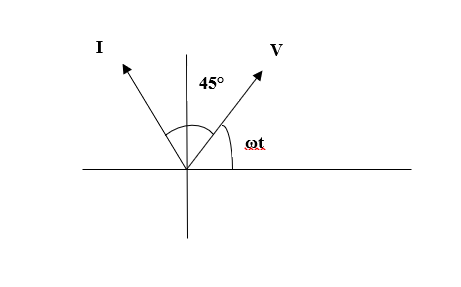
So, the phase difference between current and voltage is 45°.

Note:
Phasor diagrams are used to do mathematical operations such as addition, subtraction, multiplication etc. The calculation can include any common values such as RMS, peak values etc. Students should not get confused between vector and phasor. Vector illustrates quantity and direction whereas phasor illustrates quantity and displacement. Phasor is a rotating vector. It is very difficult to represent the relation between current and voltage using a graph, hence phasor diagrams are used.