Question

Draw a line l and take a point P which is not on the line l. Now, from point P, draw a line m such that $ m\parallel l $ ,

Answer 1

Hint: The given question revolves around the concepts of geometry and construction. We must know how to draw a line passing through a given point and parallel to another line to attempt the given problem. The slope of the two lines has to be exactly the same for the lines to be parallel to each other as parallel lines have the same directional ratios.

Complete step by step solution:
In the given problem, we have to first draw a straight line l as shown in the figure given below.

Then, we mark a point on the plane of paper which is not on the straight line l already drawn. So, we have to draw a line through the point P such that the line is drawn parallel to the former line l.

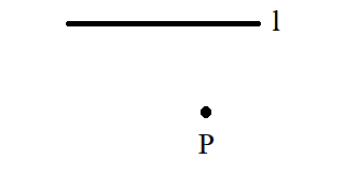
Now, we know that parallel lines are the lines that do not intersect or meet each other at any point in a plane. Parallel lines are always equidistant from each other.
So, we just take care that the perpendicular distance between the two lines remains constant throughout. To do so, we first measure the distance between the line l and the point P. Then, we mark a point without marking it as it is not asked in the question at the same distance from the line l. Then, we join point P with the new point.
Now, we draw the required line and name it as line m.

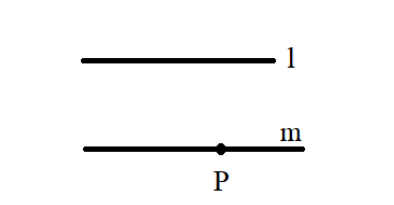
So, line m is parallel to line l. Hence, $ m\parallel l $ .
Therefore, we get the construction required as above.

Note: We should have a strong grip over the concepts of basic coordinate and analytical geometry and construction in order to deal with such questions. One must be open to mathematical ideas and construction methods to innovate and analyze the steps of construction required to get to the final result.