Question

Divide the line segment of $ {\rm{10}}\;{\rm{cm}} $ in the ratio $ 3:2 $ .

Answer 1

Hint: To solve this problem, we will draw a line segment of required length and then we will draw another ray which makes an acute angle with the line segment. According to the ratio given, we will divide this ray into a number of parts by drawing the equal arcs. After that we join the last point on the ray with the end point of the given segment. Now we can find the number of divisions according to the ratios given in the question.

Complete step-by-step answer:
We have the line of \[{\rm{10}}\;{\rm{cm}}\]. We will assume it as $ AB $ .
In order to divide the line in the ratio $ 3:2 $ we will draw a line segment $ AB $ . Next, we will draw a ray $ AX $ such that this ray is forming an acute angle with line $ AB $ .That is the angle should be less than $ {90^ \circ } $ .This can be shown as:

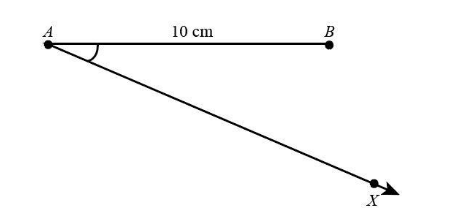
Now with the help of compass we will 5 mark points $ {A_1} $ , $ {A_2} $ , $ {A_3} $ , $ {A_4} $ and $ {A_5} $ on the ray $ AX $ , as the given ratio is $ 3:2 $ . Hence the total number of divisions we require is equal to 5. We will draw these points such that $ A{A_1} = {A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} $ . This can be done by drawing the arcs that are equal. This can be shown as:

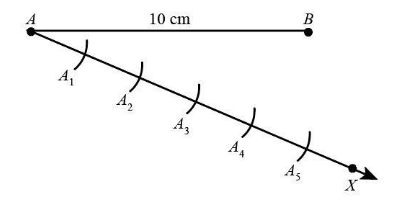
Now, we will join $ {A_5} $ with $ B $ .Since $ {A_3} $ is the third point, we will draw line passing through point $ {A_3} $ and intersecting line $ AB $ such that this line is parallel to the line $ {A_5}B $ .

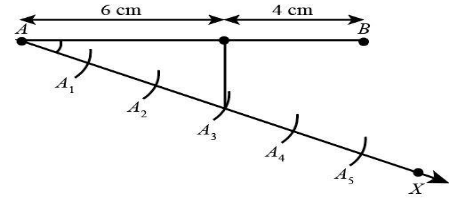
Hence the line segment is divided into $ 3:2 $ . When we will measure the length of $ AC $ it will come out to be $ {\rm{6}}\;{\rm{cm}} $ and the length of line $ BC $ will come out to be $ {\rm{4}}\;{\rm{cm}} $ .

Note: This question can be solved by the analytical and the constructional method. Here, we are using the constructional method. We can also divide the line segment from the concept of ratio and proportion. Since the ratio is given as $ 3:2 $ and we know that whenever we have given ratio as $ m:n $ we can simply use the formula $ \dfrac{{\left( {m \times x} \right) + \left( {n \times x} \right)}}{{m + n}} $ where $ x $ denotes the length of line segment and $ m $ and $ n $ denotes the terms which are in ratios.