
What is the difference between a radius and diameter?
Answer
524.1k+ views
Hint: A closed and round shaped figure is said to be a circle. It is a figure that is made up of infinitely many points, but it does not have any edge point or corners on it. It is a two dimensional figure containing both diameter and radius.
Complete step-by-step answer:
A circle is a two dimensional, closed curved figure that possesses a radius and diameter. Both radius and diameter have many applications in a circle and are very useful. They have similarities but they are very much different.
We can understand the differences between a radius of a circle and a circle’s diameter, more or less by observing the given figure.
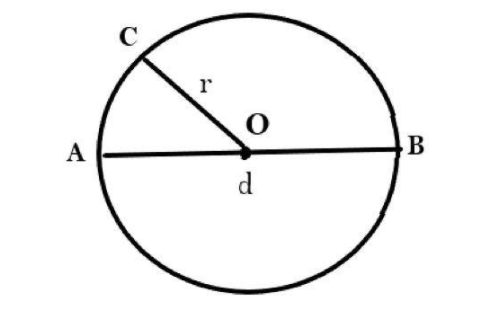
Any circle can be denoted by its center. From the figure, the center of the circle is said to be $O$, so let us refer to the circle as;
Circle $O$
In this circle $O$, there are two different line segments that have been marked, where one among them is denoted as ‘$r$’ and the other line segment is denoted as ‘$d$’. By observation we can say that one is longer than the other.
We shall list out their differences:
Note: A similarity between the radius and diameter of a circle are that they are both constructed with respect to the center of the circle. When a line is constructed from the center to any point on a circle, it becomes a radius; while diameter is constructed by tracing a line from a point on an arc of the circle to the circle’s center then continuing from the center to another point on the opposite arc of the circle.
Complete step-by-step answer:
A circle is a two dimensional, closed curved figure that possesses a radius and diameter. Both radius and diameter have many applications in a circle and are very useful. They have similarities but they are very much different.
We can understand the differences between a radius of a circle and a circle’s diameter, more or less by observing the given figure.

Any circle can be denoted by its center. From the figure, the center of the circle is said to be $O$, so let us refer to the circle as;
Circle $O$
In this circle $O$, there are two different line segments that have been marked, where one among them is denoted as ‘$r$’ and the other line segment is denoted as ‘$d$’. By observation we can say that one is longer than the other.
We shall list out their differences:
| Radius | Diameter |
| (i) While travelling around the circumference or path of the circle, the fixed length between the center and any point on the arc is said to form a radius. | (i) Any line that touches two points of the circumference is said to be a chord and the longest chord that passes through the center is termed as the diameter. |
| In given figure, the radii constructed are:\[{\mathbf{OA}},{\text{ }}{\mathbf{OB}},{\text{ }}{\mathbf{OC}}\] | In the given figure, the only diameter constructed is:\[{\mathbf{AB}}\] |
| (ii) In Mathematical terms we can write the expression of a radius as: \[{\mathbf{r}}\]So the radius is always a constant. | (ii) The expression of diameter is: \[{\mathbf{d}} = {\mathbf{2r}}\]Diameter is always twice the length of the fixed radius. |
| (iii) In terms of radius the area of a circle becomes:$\pi {r^2}$ where $r$ is the radius. | (iii) Using the diameter we can find the area of the circle like this:$\pi {(\dfrac{d}{2})^2}$, where $d = 2r$ is the diameter. |
| (iv) Any two radii along with an arc (smaller) of the circle are able to enclose an area which is commonly called as a sector. | (iv) A chord drawn by joining two points on the circle; encloses an area with the arc which is called a segment. This can be made by a diameter since it is a chord. |
| Example: If a circle has a radius of $3$, the diameter of the circle becomes $2 \times 3 = 6$. | Example: If a circle has a diameter $6$, then the circle’s radius will be $\dfrac{6}{2} = 3$. |
Note: A similarity between the radius and diameter of a circle are that they are both constructed with respect to the center of the circle. When a line is constructed from the center to any point on a circle, it becomes a radius; while diameter is constructed by tracing a line from a point on an arc of the circle to the circle’s center then continuing from the center to another point on the opposite arc of the circle.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





