Question

Diagonals PR and QS of Quadrilateral PQRS intersect each other at A. Show that
$ar\left( {\Delta PSA} \right) \times ar\left( {\Delta QAR} \right) = ar\left( {\Delta PAQ} \right) \times ar\left( {\Delta SAR} \right)$

Answer 1

Hint: As we know that the area of the triangle is given as $ar\Delta = \dfrac{1}{2} \times base \times height$ and in order to find the area of the triangle we need it’s base and height. Since the base for each of the triangles is known we just have to draw the perpendiculars on each triangle to find its height.


Complete step by step solution
Given:
A Quadrilateral PQRS having diagonals PR and QS respectively, both of the diagonals intersect each other at a point A.
So first we draw a perpendicular SM from point S to a point on diagonal M, similarly another perpendicular QN from point Q to a point on diagonal N.
.

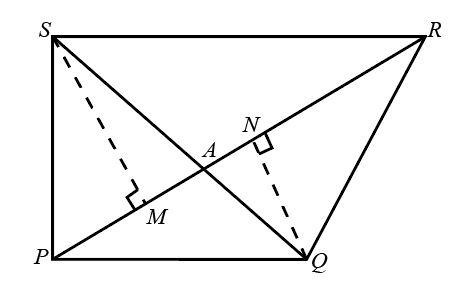
Now we have the height of each triangle and we can easily calculate the area of the triangles.
So, using the formula the area of the $\Delta PSA$ can be given as,
$ar\left( {\Delta PSA} \right) = \left( {\dfrac{1}{2} \times PA \times SM} \right)$……(1)
Similarly, we know the area of the $\Delta QAR$ is given as,
$ar\left( {\Delta QAR} \right) = \left( {\dfrac{1}{2} \times AR \times QN} \right)$……(2)
The area of the $\Delta SAR$ is given as,
$ar\left( {\Delta SAR} \right) = \left( {\dfrac{1}{2} \times AR \times SM} \right)$……(3)
And, the area of the $\Delta PAQ$ is given as,
$ar\left( {\Delta PAQ} \right) = \left( {\dfrac{1}{2} \times PA \times QN} \right)$……(4)
Now according to the question by equating the sum of equation (1) and (2) with sum of equation (3) and (4), we get,
$\begin{array}{c}
ar\left( {\Delta PSA} \right) \times ar\left( {\Delta QAR} \right) = ar\left( {\Delta PAQ} \right) \times ar\left( {\Delta SAR} \right)\\
\left( {\dfrac{1}{2} \times PA \times SM} \right) \times \left( {\dfrac{1}{2} \times AR \times QN} \right) = \left( {\dfrac{1}{2} \times PA \times QN} \right) \times \left( {\dfrac{1}{2} \times AR \times SM} \right)\\
\dfrac{1}{4} \times PA \times SM \times AR \times QN = \dfrac{1}{4} \times PA \times QN \times AR \times SM
\end{array}$
Hence, it is proved that $ar\left( {\Delta PSA} \right) \times ar\left( {\Delta QAR} \right) = ar\left( {\Delta PAQ} \right) \times ar\left( {\Delta SAR} \right)$.


Note: In the formula used to calculate the area of the triangle we always take the perpendicular to the base of the triangle as height of the triangle. For example, in the formula used for the area of the triangle $\left( {\Delta SAR} \right)$ we have used SM as the height of the triangle because it is perpendicular to the base of the triangle.