Question

Diagonals of a trapezium PQRS intersect each other at the point O, $ \text{PQ}\parallel \text{RS} $ and $ \text{PQ}\,\text{=}\,\text{3RS} $ . Find the ratio of the areas of the triangles POQ and ROS.

Answer 1

Hint: n this question, we need to draw the figure and then use AA criterion for similar triangles for proving the similarity and further solving the problem to find the ratio of areas of triangles.

Complete step-by-step answer:
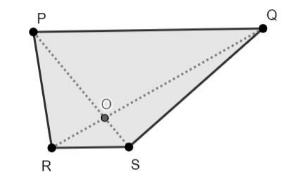
We have, a trapezium PQRS with $ \text{PQ}\parallel \text{RS} $ and $ \text{PQ}\,\text{=}\,\text{3RS} $ , the diagonals in the trapezium intersect each other at point O.
Let us first draw the diagram to understand the given conditions,

Here, due to the diagonals PS and RQ bisecting each other at O, we have triangles POQ and ROS.
Now, we have $ \angle \text{POQ}\cong \angle \text{ROS} $ ……… (opposite angles are congruent)
Also, $ \angle \text{PQO}\cong \angle \text{SRO} $ …………………... (alternate angles are congruent to each other)
Therefore, we can say that $ \vartriangle \text{POQ}\sim \vartriangle \text{ROS} $ (By AA criterion for similar triangles)
This means that triangles POQ and ROS are similar to each other.
By the property of similarity of triangles, we get
\[\dfrac{area\left( \vartriangle \text{POQ} \right)}{area\left( \vartriangle \text{ROS} \right)}={{\left( \dfrac{\text{PQ}}{\text{RS}} \right)}^{2}}\]............... (i)
We know, $ \text{PQ}\,\text{=}\,\text{3RS} $ ................ (ii) (given)
Divide the equation (ii) by RS on both the sides of the equation
 $ \dfrac{\text{PQ}}{\text{RS}}=\dfrac{3}{1} $ ....................................(iii)

Substitute equation (iii) in the equation (i), we get
\[\dfrac{area\left( \vartriangle \text{POQ} \right)}{area\left( \vartriangle \text{ROS} \right)}={{\left( \dfrac{3}{1} \right)}^{2}}\]
After separating the square to the numerator and denominator, we get
\[\dfrac{area\left( \vartriangle \text{POQ} \right)}{area\left( \vartriangle \text{ROS} \right)}=\dfrac{{{\left( 3 \right)}^{2}}}{{{\left( 1 \right)}^{2}}}\]
Now, solve further to find the ratio between the areas of triangles POQ and ROS
\[\dfrac{area\left( \vartriangle \text{POQ} \right)}{area\left( \vartriangle \text{ROS} \right)}=\dfrac{9}{1}\]
Hence, the ratio of triangles POQ and ROS is 9:1

Note: The drawing of the figure according to the conditions mentioned in the question is important to avoid any mistakes. One pair sides of trapezium are parallel to each other and the other pair are not parallel. If the question for area of trapezium is asked, you can use, ‘area of the trapezium = $ \dfrac{1}{2}h\left( a+b \right) $ ’ where, h = height of the trapezium or the distance between the two parallel sides or bases, a and b are the value of the two parallel sides or bases.