Question

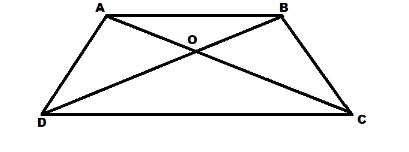
Diagonals AC and BD of a trapezium ABCD with AB ll DC intersect each other at O. Prove that Area of Δ (AOD) = Area of Δ (COB) and Δ AOB and Δ COD are similar.

Answer 1

Hint: To prove the above two things we need to remember two basic things. First, triangles with the same base and between the same parallels are equal in area so area of Δ (ADC) = area of Δ (BDC) and second, two triangles are said to be similar if any two angles of both the triangles are equal. Using these two concepts we can easily solve the question.

Complete step-by-step answer:
Given:
A trapezium ABCD having its sides AB & DC parallel to each other. And its two diagonal AC & BD intersecting each other at O.
To prove:
Area of Δ (AOD) = Area of Δ (COB)
Δ AOB and Δ COD are similar.

To prove:
Area of Δ (AOD) = Area of Δ (COB)
First, we need to know that triangles with the same base and between the same parallels are equal in area so area of Δ (ADC) = area of Δ (BDC).
Now, if we deduct the area of Δ (ODC) from both the Δ (ADC) and Δ (BDC)
Area of Δ (ADC) - Area of Δ (ODC) = Area of Δ (BDC) - Area of Δ (ODC)
i.e. Area of Δ (AOD) = Area of Δ (COB)
Hence proved, Area of Δ (AOD) = Area of Δ (COB)
To prove:
Δ AOB and Δ COD are similar
We need to use the Angle-Angle similarity method according to which two triangles are said to be similar if any two angles of both the triangles are equal.
Now since $ \angle AOB $ and $ \angle DOC $ are vertically opposite angles,
 $ \Rightarrow \angle AOB = \angle DOC $
And, since AB ll DC with AC as traversal, $ \angle OCD $ and $ \angle OAB $ are alternate angles.
Hence,
 $ \Rightarrow \angle OCD = \angle OAB $
Hence proved, Δ AOB and Δ COD are similar triangles.

Additional Information:
There are a total three triangle similarity theorems, known as Angle - Angle (AA), Side - Angle - Side (SAS) or Side - Side - Side (SSS), to determine if two triangles are similar.

Note: We have to remember the above theorems because you will come across them occasionally but don’t confuse them and always use them accordingly. And also don’t confuse in selecting the alternate angles because alternate angles are always shaped by two parallel lines crossed by a transversal.