Question

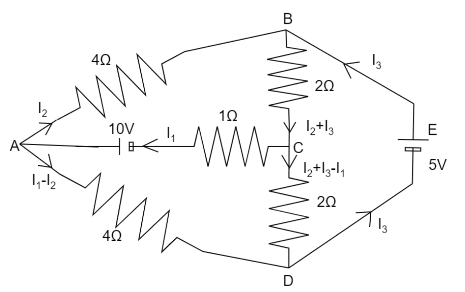
Determine the current in each branch of the network.

Answer 1

Hint: with the help of kirchhoff’s law we can solve this problem. Kirchhoff’s Current law states that, the total of the currents in a junction is equal to the sum of currents outside the junction. Kirchhoff’s Voltage Law states that, the sum of the voltages around the closed loop is equal to null.

Complete step by step answer:
In the given network of resistors, we have been given two batteries.
The current from the battery of $ 10V $ is $ {I_1} $ at junction A the current is divided as per the current law. So, in branch AB current is $ {I_2} $ and in branch AD current is $ {I_1} - {I_2} $ . the current from second battery of $ 5V $ to the junction B is $ {I_3} $ therefore current in branch BC will be $ {I_2} + {I_3} $ . at junction C since in branch AC there is $ {I_1} $ current so for branch CD the current will be $ {I_2} + {I_3} - {I_1} $ . now from junction A current $ {I_1} - {I_2} $ is coming so at junction D after the current will combine only $ {I_3} $ will go back to the battery.
Now for loop ACDA, using Kirchhoff’s second (voltage) law which states that in a closed electric circuit the sum of the emf is equal to the sum of the product of resistance and currents flowing through them.

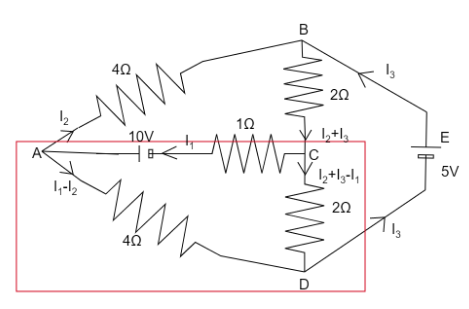
 $ 10 = ({I_1} - {I_2})4 - ({I_2} + {I_3} - {I_1})2 + {I_1}(1) $
 $ \Rightarrow 7{I_1} - 6{I_2} - 2{I_3} = 10 $ …………….. $ (1) $
For loop ABCA

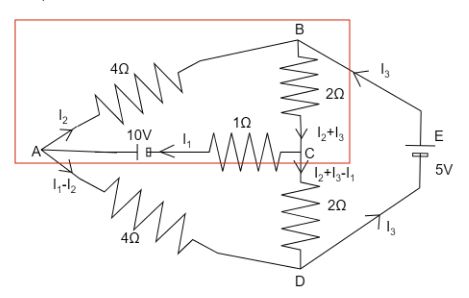
 $ - 10 = - {I_2}(4) - ({I_2} + {I_3})(2) - I(1) $
 $ \Rightarrow {I_1} + 6{I_2} + 2{I_3} = 10 $ ……………………. $ (2) $
In loop BCDEB

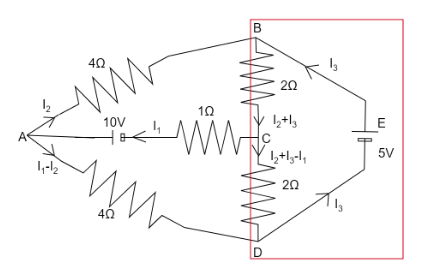
 $ 5 = ({I_2} + {I_3})(2) + ({I_2} + {I_3} - {I_1})(2) $
 $ - 2{I_1} + 4{I_2} + 4{I_3} = 5 $ ……………… $ (3) $
Adding equation $ (1) $ and $ (2) $ we get,
 $ 8{I_1} = 20 $
 $ \Rightarrow {I_1} = 2.5A $
Putting value of $ {I_1} $ in equation $ (1) $ we get
 $ 7(2.5) - 6{I_2} - 2{I_3} = 10 $
 $ \Rightarrow 6{I_2} + 2{I_3} = 7.5 $ ……………………. $ (4) $
Putting value of $ {I_1} $ in equation $ (3) $ we get
 $ - 2(2.5) + 4{I_2} + 4{I_3} = 5 $
 $ \Rightarrow 2{I_2} + 2{I_3} = 5 $ ……………………. $ (5) $
Solving equation $ (4) $ and $ (5) $
 $ 4{I_2} = 2.5 $
 $ \Rightarrow {I_2} = \dfrac{5}{8}A $
Finally with this find $ {I_3} $ from equation $ (5) $
 $ 2\left( {\dfrac{5}{8}} \right) + 2{I_3} = 5 $
 $ \Rightarrow {I_3} = \dfrac{{15}}{8}A $ .

Note:
Because of the charging of energy at the emf source, the source of emf (E) signs positive as the current moves from low to high. Similarly, if the current changes from high to low voltage ( $ + $ to $ - $ ), the source of emf (E) signs negative due to the emf source's energy being depleted.