Question

Derive the relation between force applied and acceleration produced using Newton’s second law of motion.
Represent the following graphically.
a) Momentum versus velocity, when mass is fixed.
b) Momentum versus mass when velocity is constant.

Answer 1

Hint: The second law of motion provides us a method to estimate the force acting on an object as a product of the object's mass and the object's acceleration, which is the change in velocity concerning time. Force is the change of momentum rate. For a fixed mass, force is mass times acceleration.

Complete step-by-step solution:
We consider an object of mass $m$ having an initial velocity $u$; after traveling for $t$ time, it attains final velocity $v$.
Initial momentum, $p_{1} = mu$
Final momentum, $p_{2} = mu$
Change in momentum = $p_{2} - p_{1} = mv – mu$
Total time taken = t
There is an applied force $F$.
According to Newton’s second law of motion,
Applied Force is equal to the rate of change of momentum.
$F = \dfrac{p_{2} - p_{1} }{t}$
$\implies F = \dfrac{mv - mu }{t}$
$\implies F = \dfrac{m(v – u) }{t}$
Using first equation of motion,
$v = u + at$
We get, $a = \dfrac{v-u}{t}$
Therefore, we get,
$F = ma$
This is the relation between force applied and acceleration.
Momentum, $p = mv$
Where, m is the mass of the body.
v is the velocity of the body.
a) Momentum versus velocity, when mass is fixed.
$ p \propto v$

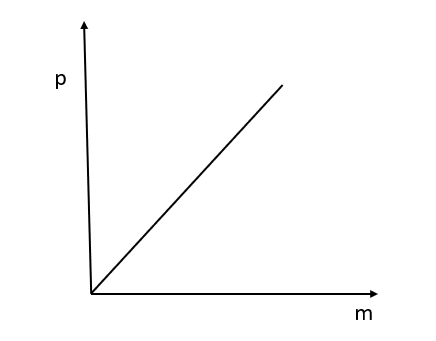
b) Momentum versus mass when velocity is constant.
$p \propto m$

Note:Unlike the first law of motion, Newton’s second law of motion concerns the behaviour of objects for which all fundamental forces are unbalanced. The second law is more quantitative and is utilized extensively to determine what happens in conditions involving a force.