Question

Current shown in the figure is:

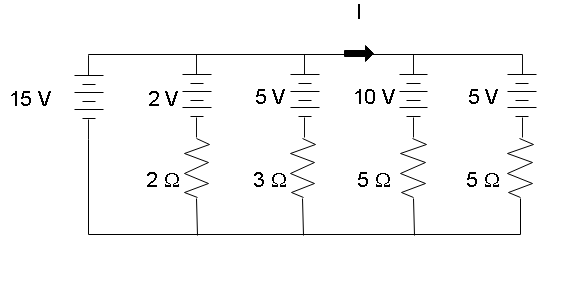
A) 7 A
B) 2 A
C) 5 A
D) 3 A

Answer 1

Hint: In this solution, we will use Kirchhoff’s current and voltage loop law to determine the current in different branches of the circuit. According to Kirchhoff’s current law, the current entering the leaving the junction must be the same.

Formula used:
-Kirchhoff’s voltage law: $\sum {\Delta V = 0} $ which implies that the net potential drop in a loop is 0
- Kirchhoff’s current law: $\sum\limits_{junction} {i = 0} $ which implies that the net current at a junction is also zero.

Complete step by step answer:
In the circuit given to us, let us start by naming the currents in different branches of the circuit.
The potential drop across the battery will be negative when the direction of current is assumed to be from its negative to the positive terminal and positive when going from a positive to a negative terminal. The voltage drop across a resistor will be the product of the current in the resistance and the value of the resistance as determined from ohm’s law $(\Delta V = iR)$.
Starting with the loop ABCDA, we can use Kirchhoff’s voltage law and write
$ - 15 + 2{i_2} + 2 = 0$
Solving for ${i_2}$, we get
${i_2} = \dfrac{{13}}{2}A$
Now in the loop CDEFC, we can use Kirchhoff’s voltage law and write
$2 + 2{i_2} - 5 - 3{i_3} = 0$
Substituting the value of ${i_2} = \dfrac{{13}}{2}A$, we can solve for ${i_3}$ as
$ - 3{i_3} = 3 - 13$
$ \Rightarrow {i_3} = \dfrac{{10}}{3}$
Now in the loop EFGHE,we can use Kirchhoff’s voltage law and write
$ - 5 - 3{i_3} + 5{i_5} + 10 = 0$
Substituting the value of ${i_3} = \dfrac{{10}}{3}$, we can solve the above equation for ${i_5}$ as
$5{i_5} = 5$
$ \Rightarrow {i_5} = 1$
In the final loop GHIJG, we can use Kirchhoff’s voltage law and write
$5{i_5} + 10 - 5 - 5{i_4} = 0$
Substituting the value of ${i_5} = 1$, we can solve the above equation for ${i_4}$ as
$5{i_4} = 10$
$ \Rightarrow {i_4} = 2$
Now from the diagram, we can see that at the junction point ‘H’, the current $I$ is entering and the current ${i_4} + {i_5}$ is exciting so from Kirchhoff’s current law, we can write
$I = {i_4} + {i_5}$
$\therefore I = 3A$ which corresponds to option (D).

Note: The direction of currents assumed in the image has been done intuitively. Even if we chose the opposite direction of the current, we will get the same magnitude but a negative sign of the current would indicate the direction of the current is opposite to what we have assumed. While using Kirchhoff’s voltage law, we should be careful that potential drop will only occur across resistors and potential cells and not in the wire which is why we can only find the current values corresponding to branches containing resistors and batteries directly.