Answer
Verified438.3k+ views
Hint: A straight line in the form \[y=mx+c\] has slope m and y-intercept c. We can graph any straight line using any two points lying on it. Now we have to find the points lying on the straight line and draw the graph.
As per the given question, we have to graph the given straight line by creating a table and plot the points.
Complete step by step answer:
To find the points we have to substitute some x values in the straight line then we get the value of y.
Let \[x=-2\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( -2 \right)-1=-4-1=-5\]
Now \[x=-1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( -1 \right)-1=-2-1=-3\]
Now \[x=0\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 0 \right)-1=0-1=-1\]
Now \[x=1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 1 \right)-1=2-1=1\]
Now \[x=1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 2 \right)-1=4-1=3\]
Now we draw a table and enter these points
Now we plot these points on a graph and join them with a straight line.
The graph of \[y=2x-1\] is shown below:
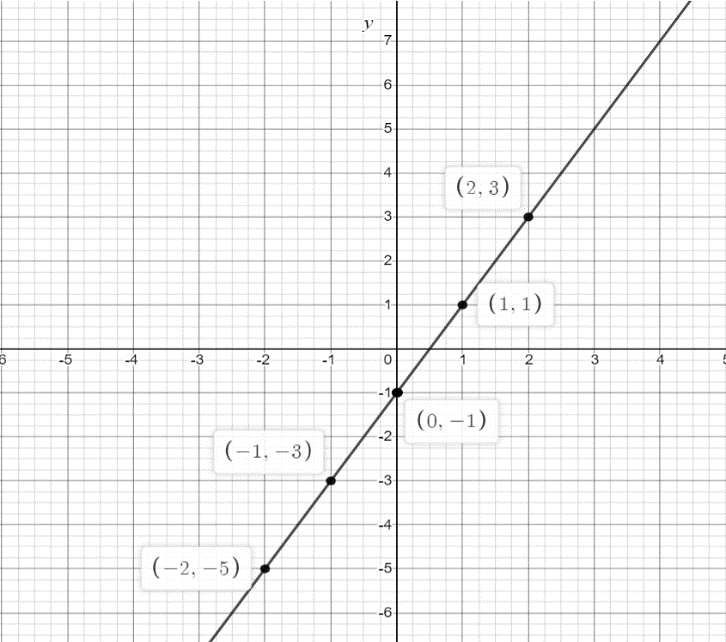
Note: In order to solve these types of problems, we need to have knowledge over straight lines. We should know about how to graph a straight line. We can draw the graph of \[y=ax+b\] from the simple graph \[y=x\]. We need to modify the \[y=x\] graph by shifting and scaling methods. It is a better idea to modify the graph of \[y=x\] in such a manner that we get the required graph by going from left side to right side of the equation \[y=2x-1\]. We should avoid calculation mistakes to get the correct solution.
As per the given question, we have to graph the given straight line by creating a table and plot the points.
Complete step by step answer:
To find the points we have to substitute some x values in the straight line then we get the value of y.
Let \[x=-2\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( -2 \right)-1=-4-1=-5\]
Now \[x=-1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( -1 \right)-1=-2-1=-3\]
Now \[x=0\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 0 \right)-1=0-1=-1\]
Now \[x=1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 1 \right)-1=2-1=1\]
Now \[x=1\] then the value of y is
\[\Rightarrow \]\[y=2x-1=2\left( 2 \right)-1=4-1=3\]
Now we draw a table and enter these points
| x | y | \[\left( x,y \right)\] |
| -2 | -5 | \[\left( -2,-5 \right)\] |
| -1 | -3 | \[\left( -1,-3 \right)\] |
| 0 | -1 | \[\left( 0,-1 \right)\] |
| 1 | 1 | \[\left( 1,1 \right)\] |
| 2 | 3 | \[\left( 2,3 \right)\] |
Now we plot these points on a graph and join them with a straight line.
The graph of \[y=2x-1\] is shown below:
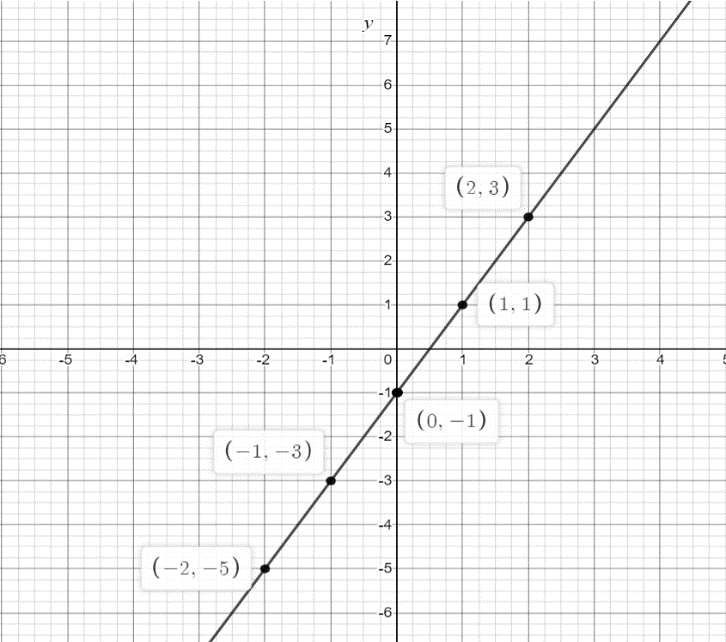
Note: In order to solve these types of problems, we need to have knowledge over straight lines. We should know about how to graph a straight line. We can draw the graph of \[y=ax+b\] from the simple graph \[y=x\]. We need to modify the \[y=x\] graph by shifting and scaling methods. It is a better idea to modify the graph of \[y=x\] in such a manner that we get the required graph by going from left side to right side of the equation \[y=2x-1\]. We should avoid calculation mistakes to get the correct solution.