Question

Construct Rhombus MATH with $AT = 4cm$ and $\angle MAT = 120^\circ $.

Answer 1

Hint: We have to construct a rhombus whose one side and one angle is known. Now, a rhombus has all the sides equal, so $MA = AT = TH = MH = 4cm$. Now, rhombus has equal opposite angles so,
$\angle MAT = \angle MHT = 120^\circ $ and $\angle ATH = \angle AMH = x$. The sum of all the angles of any quadrilateral is equal to 360. Using this we can find the remaining two angles. Hence, we now have every data for constructing our rhombus.

Complete step by step solution:
In this question, we have to construct a Rhombus MATH and we are given the following parameters.
$ \Rightarrow AT = 4cm$
$ \Rightarrow \angle MAT = 120^\circ $
First of all, let us see the properties of a rhombus.
$ \Rightarrow $A rhombus has all the sides equal to each other.
Here, we have $AT = 4cm$. Therefore, $MA = AT = TH = MH = 4cm$.
$ \Rightarrow $A rhombus has equal opposite angles.
Here, we have $\angle MAT = 120^\circ $. So, therefore angle opposite to it will be $\angle MHT$ and it will be equal to $120^\circ $.
Let $\angle AMH = x$. So, therefore $\angle ATH$ will also be equal to $x$.
Now, we know that the sum of all the angles in any quadrilateral is equal to $360^\circ $.
Therefore,
$
   \Rightarrow \angle MAT + \angle ATH + \angle MHT + \angle AMH = 360 \\
   \Rightarrow 120 + x + 120 + x = 360 \\
   \Rightarrow 2x = 360 - 240 \\
   \Rightarrow 2x = 120 \\
   \Rightarrow x = 60 \\
 $
Hence, $\angle ATH = \angle AMH = 60^\circ $.
Now, we have all the data for constructing our rhombus.
$ \Rightarrow MA = AT = TH = MH = 4cm$
$ \Rightarrow \angle ATH = \angle AMH = 60^\circ $
$ \Rightarrow \angle MAT = \angle MHT = 120^\circ $
Steps for constructing Rhombus:
Step 1:
Draw a horizontal line segment AT of length 4cm.

Step 2:
Place the midpoint of the protractor at point A and mark a point at $120^\circ $ and then join the point with the vertex. Make sure that the point is at a distance 4 cm from point A.

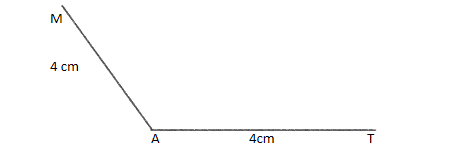
Step 3:
Place the midpoint of protractor at point M and mark a point at $60^\circ $ and then join the point with the vertex M. Make sure that the distance between this point and point M is 4cm.

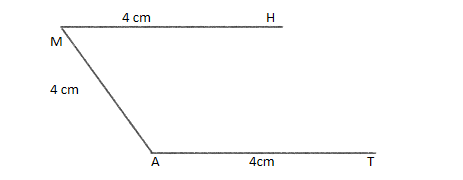
Step 4:
Now, simply draw a line segment from point H to point T. Measure the length and angle they must be equal to 4 cm and $120^\circ $.

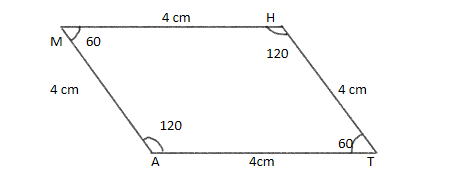
Hence, we have constructed the required rhombus.

Note:
As all the sides of a rhombus are equal, its perimeter is given by
$ \Rightarrow $Perimeter of rhombus$ = 4a$
Therefore, the perimeter of a rhombus will be equal to
$ \Rightarrow $Perimeter$ = 4 \times 4 = 16cm$