Question

Construct a triangle ABC in which$BC = 8\,{\rm{cm,}}\angle B{\rm{ = 45}}^\circ \,{\rm{and AB - AC = 3}}{\rm{.5}}\,{\rm{cm}}$.

Answer 1

Hint: To construct this triangle use the method of construction of a triangle with one side, one angle and difference of other two sides.
Given, one side of triangle is$BC = 8\,{\rm{cm,}}\angle B{\rm{ = 45}}^\circ \,{\rm{and AB - AC = 3}}{\rm{.5}}\,{\rm{cm}}$.

Complete Step-by-step Solution
Step 1. Draw the baseline of the triangle as $BC = 8\,{\rm{cm}}$.

Step 2. Now draw an angle of $45^\circ $ from point B. To make an angle of $45^\circ $, first make it perpendicular on line BC and then draw the bisector of the right angle, this will give the $\angle B = 45^\circ $.

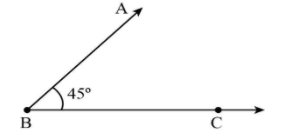
Step 3. Open the compass and fill the distance ${\rm{AB}} - {\rm{AC}} = {\rm{3}}{\rm{.5}}\,{\rm{cm}}$ and draw an arc from point B at ray BX, mark this point as D.

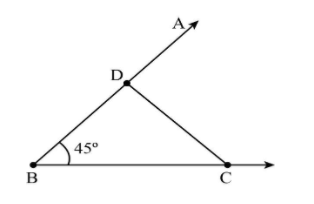
Step 4. Join points C and D.

Step 5. Now draw a perpendicular bisector of line CD, which intersects the ray BX at point A.

Step 6. Now join AC.

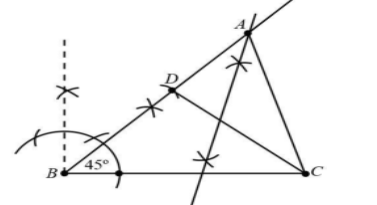
Hence, $\Delta ABC$ is a required triangle.

Note: While making arc of difference of the sides that is given, remember that difference is positive so arc is always made on the upper side of the ray BX.