Question

Construct a trapezium KITE in which \[KI\parallel ET\], \[\angle K={{75}^{\circ }}\], \[\angle T={{90}^{\circ }}\], $KI=6cm$ $KE=3.8cm$ and $ET=4.5cm$.

Answer 1

Hint: Firstly, we have to draw the base KI of the trapezium of length $6cm$. Then, we need to draw a line at an angle of ${{75}^{\circ }}$ at the vertex K by bisecting the angles of ${{60}^{\circ }}$ and ${{90}^{\circ }}$. Then, with the help of the ruler, we need to mark the point E on the ${{75}^{\circ }}$ line at a distance of $3.8cm$ from K. Similarly, we need to draw the angle of ${{90}^{\circ }}$ at the vertex I and mark the point T on the ${{90}^{\circ }}$ line at a distance of $4.5cm$ from E. Finally, on joining the points E and T we will get the required trapezium KITE.

Complete step by step solution:
Step I: Draw the base KI of length $6cm$.

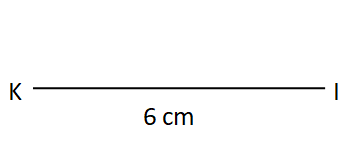
Step II: With K as centre a convenient radius, draw an arc.

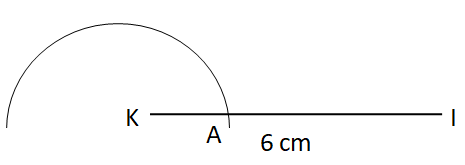
Step III: Now, with A as centre and the same radius, draw an arc cutting the original arc at B.

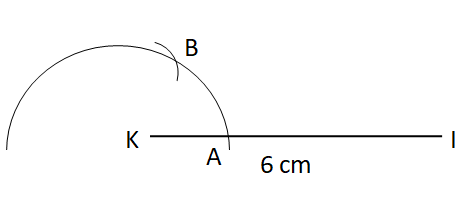
Step IV: With B as centre and the same radius, draw an arc cutting the original arc at C.

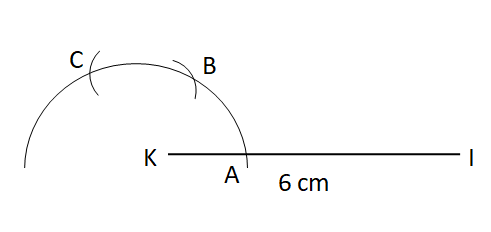
Step V: Now, with B and C as centers and the same radius, draw two arcs cutting each other at D.

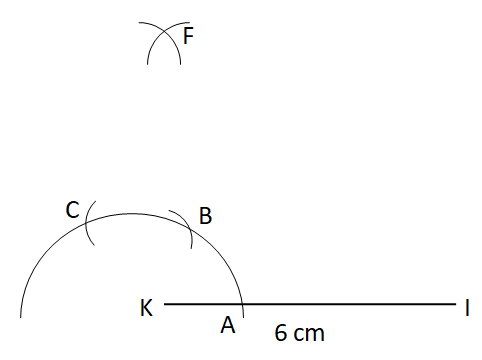
Step VI: With B and F as centers and same radius, draw two arcs cutting at G to obtain the angle of ${{75}^{\circ }}$. Join K and G.

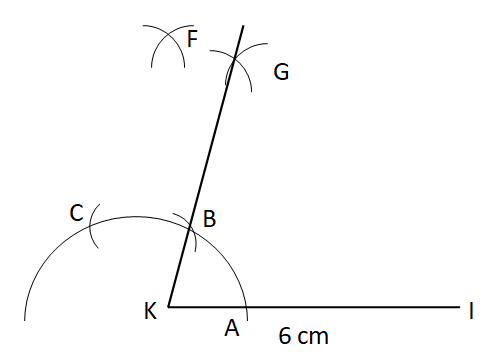
Step VII: Similarly, draw an angle of ${{90}^{\circ }}$ at I.

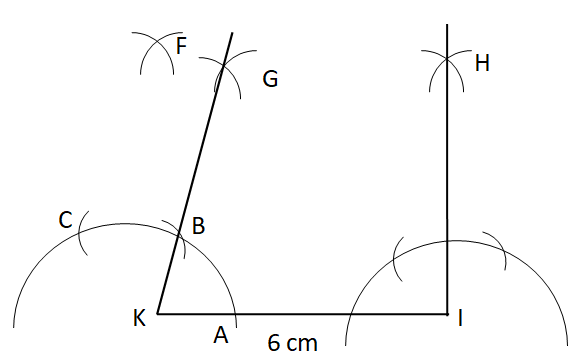
Step VIII: With the help of the ruler, mark the points E on KG at the distance of $3.8cm$.

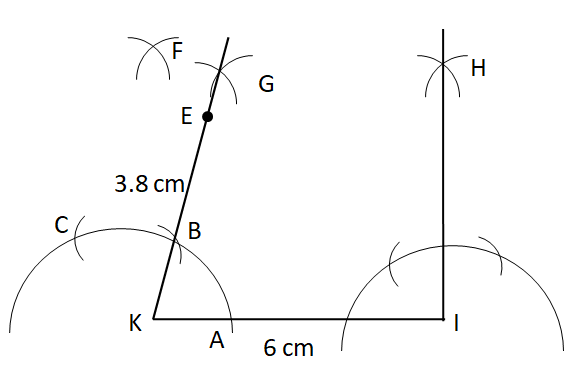
Step IX: With E as centre and radius $4.5cm$, draw an arc cutting IH at T.

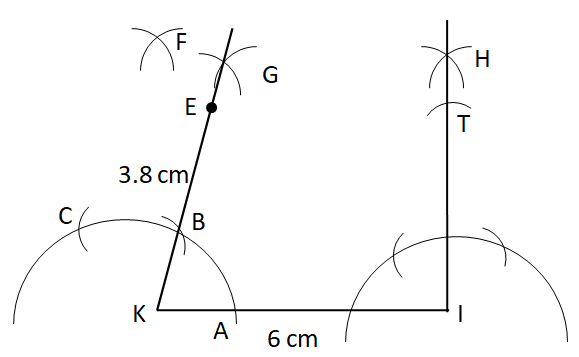
Step X: Finally, join E and T.

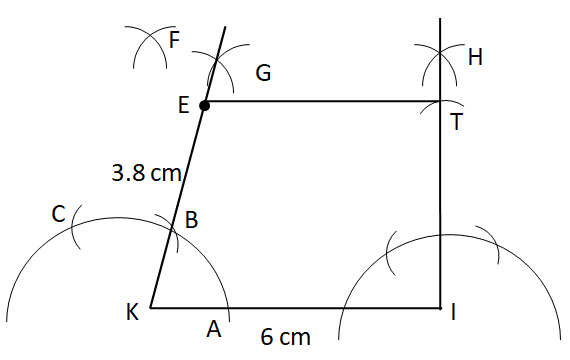
Hence, the trapezium KITE is constructed.

Note: In the given question, the angle T is given to be equal to ${{90}^{\circ }}$, but we have drawn the ${{90}^{\circ }}$ angle at I. This is since \[KI\parallel ET\] as given in the question. All the arcs must be drawn very lightly so as to obtain perfect angles.