
Construct a $\Delta ABC$ in which CA = 6cm, AB = 5cm and $\angle BAC={{45}^{\circ }}$, then construct a triangle whose sides are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
Answer
575.7k+ views
Hint: First, we will draw a side of $\Delta ABC$, then will draw the given angle corresponding to the side which we had drawn. Then, using the compass, we will make an arc according to the given side and join all the points obtained. Then, according to this question, we will draw another triangle $\Delta PQR$. So, with reference to the sides of $\Delta ABC$, we will get the sides of the $\Delta PQR$. For constructing the $\Delta PQR$, we will first draw one side, then using the compass, we will mark arcs according to the length of the sides, and then finally join all the points to complete the triangle.
Complete step by step answer:
We have been given in the question that we have to construct a $\Delta ABC$ in which CA = 6cm, AB = 5cm and $\angle BAC={{45}^{\circ }}$, then we also have to construct a triangle whose sides are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
So, we will first construct the $\Delta ABC$ and for doing so, we will follow a few steps as mentioned below.
Step 1: First, we will draw a line segment AB = 5cm, which is one of the sides of the $\Delta ABC$.

Step 2: We are given that $\angle BAC={{45}^{\circ }}$, so we will use a protractor and we will place its center on point A and measure and mark ${{45}^{\circ }}$.
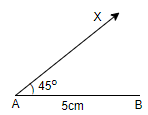
Step 3: Another side of the $\Delta ABC$ given to us is the side AC = 6cm. So, by taking 6 cm on the compass and on placing the compass at point A, we will cut an arc on the line AX and we can name the point of intersection of line AX and the arc as point C.
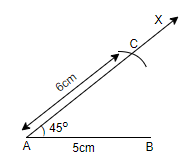
Step 4: Now, we will join the points B and C. So, our construction of $\Delta ABC$ will be complete. Hence, we get $\Delta ABC$ as,
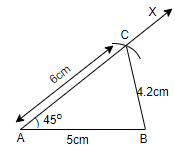
Now, when we measure the side BC, we get that BC = 4.2cm.
According to the question, we get that the sides of $\Delta PQR$ are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
So, we can say that the corresponding sides are AB and PQ, BC and QR, and AC and PR. So, we can write,
$\begin{align}
& PQ=\dfrac{3}{5}AB=\dfrac{3}{5}\times 5=3cm \\
& QR=\dfrac{3}{5}BC=\dfrac{3}{5}\times 4.2=2.52cm \\
& PR=\dfrac{3}{5}AC=\dfrac{3}{5}\times 6=3.6cm \\
\end{align}$
Hence, we get the sides of $\Delta PQR$ as PQ = 3cm, QR = 2.52cm and PR = 3.6cm.
So, we will construct $\Delta PQR$ and we will follow a few steps mentioned below to do so.
Step 1: We will draw a line segment PQ = 3cm, which is one of the sides of $\Delta PQR$.
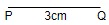
Step 2: We have got the length of side PR as 3.6cm. So, taking 3.6cm on the compass and placing the compass at point P, we will simply draw an arc.
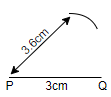
Step 3: We also have another side, that is, QR = 2.52cm. So, taking 2.52cm on the compass and placing the compass at point Q, we will draw an arc, such that it cuts the previously drawn arc. And we will name the point of intersection of both the arcs as point R.
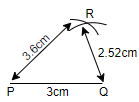
Step 4: Now, we will join the points P and R and also the points Q and R. So, with this, the construction of $\Delta PQR$ will be complete.
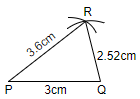
Hence, we have constructed $\Delta ABC$ in which CA = 6cm, AB = 5cm and $\angle BAC={{45}^{\circ }}$, and also constructed a triangle whose sides are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
Note: In the construction of $\Delta ABC$, for making an angle of ${{45}^{\circ }}\left( \angle BAC \right)$, we can also use the compass. So, one can do so as follows.
Step 1: Draw the line segment AB and then by using a compass and placing it at point A, we will draw an arc of any measurement and the point where the arc cuts the line AB, we will name it as X.
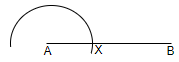
Step 2: Now, by keeping the compass at point X, with the same measurement, we will cut an arc on the previously drawn arc and name the point of intersection of the two arcs as Y. Then, by joining the points X and Y, an angle of ${{60}^{\circ }}$ is made.
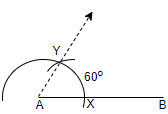
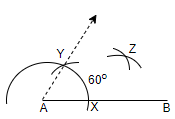
Step 3: Now, we will bisect the drawn angle.
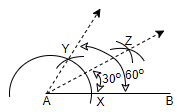
For that, we will place the compass with any measurement at point X, draw an arc, and then, place the compass with the same measurement at point Y and draw an arc, such that it cuts the previously drawn arc and we will name the intersection point of both the arcs as point Z.
Step 4: Now, by joining the points A and Z, we get the bisection of the angle, ${{60}^{\circ }}$, which is equal to ${{30}^{\circ }}$.
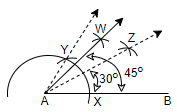
Step 5: Now, we will bisect the angle ZAY, using the same method as mentioned in step 3. So, we will get an angle of ${{45}^{\circ }}$ between the line AB and the bisection line of angle ZAY, which is the line AW.
Also, while solving this question, the students must ensure that they follow each and every step of construction and must take the correct measurements. And the students must mark the required points, sides and angles in the figure in order to make the construction perfect.
Complete step by step answer:
We have been given in the question that we have to construct a $\Delta ABC$ in which CA = 6cm, AB = 5cm and $\angle BAC={{45}^{\circ }}$, then we also have to construct a triangle whose sides are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
So, we will first construct the $\Delta ABC$ and for doing so, we will follow a few steps as mentioned below.
Step 1: First, we will draw a line segment AB = 5cm, which is one of the sides of the $\Delta ABC$.

Step 2: We are given that $\angle BAC={{45}^{\circ }}$, so we will use a protractor and we will place its center on point A and measure and mark ${{45}^{\circ }}$.

Step 3: Another side of the $\Delta ABC$ given to us is the side AC = 6cm. So, by taking 6 cm on the compass and on placing the compass at point A, we will cut an arc on the line AX and we can name the point of intersection of line AX and the arc as point C.

Step 4: Now, we will join the points B and C. So, our construction of $\Delta ABC$ will be complete. Hence, we get $\Delta ABC$ as,

Now, when we measure the side BC, we get that BC = 4.2cm.
According to the question, we get that the sides of $\Delta PQR$ are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
So, we can say that the corresponding sides are AB and PQ, BC and QR, and AC and PR. So, we can write,
$\begin{align}
& PQ=\dfrac{3}{5}AB=\dfrac{3}{5}\times 5=3cm \\
& QR=\dfrac{3}{5}BC=\dfrac{3}{5}\times 4.2=2.52cm \\
& PR=\dfrac{3}{5}AC=\dfrac{3}{5}\times 6=3.6cm \\
\end{align}$
Hence, we get the sides of $\Delta PQR$ as PQ = 3cm, QR = 2.52cm and PR = 3.6cm.
So, we will construct $\Delta PQR$ and we will follow a few steps mentioned below to do so.
Step 1: We will draw a line segment PQ = 3cm, which is one of the sides of $\Delta PQR$.
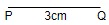
Step 2: We have got the length of side PR as 3.6cm. So, taking 3.6cm on the compass and placing the compass at point P, we will simply draw an arc.

Step 3: We also have another side, that is, QR = 2.52cm. So, taking 2.52cm on the compass and placing the compass at point Q, we will draw an arc, such that it cuts the previously drawn arc. And we will name the point of intersection of both the arcs as point R.

Step 4: Now, we will join the points P and R and also the points Q and R. So, with this, the construction of $\Delta PQR$ will be complete.

Hence, we have constructed $\Delta ABC$ in which CA = 6cm, AB = 5cm and $\angle BAC={{45}^{\circ }}$, and also constructed a triangle whose sides are $\dfrac{3}{5}$ of the corresponding sides of $\Delta ABC$.
Note: In the construction of $\Delta ABC$, for making an angle of ${{45}^{\circ }}\left( \angle BAC \right)$, we can also use the compass. So, one can do so as follows.
Step 1: Draw the line segment AB and then by using a compass and placing it at point A, we will draw an arc of any measurement and the point where the arc cuts the line AB, we will name it as X.

Step 2: Now, by keeping the compass at point X, with the same measurement, we will cut an arc on the previously drawn arc and name the point of intersection of the two arcs as Y. Then, by joining the points X and Y, an angle of ${{60}^{\circ }}$ is made.

Step 3: Now, we will bisect the drawn angle.
For that, we will place the compass with any measurement at point X, draw an arc, and then, place the compass with the same measurement at point Y and draw an arc, such that it cuts the previously drawn arc and we will name the intersection point of both the arcs as point Z.

Step 4: Now, by joining the points A and Z, we get the bisection of the angle, ${{60}^{\circ }}$, which is equal to ${{30}^{\circ }}$.

Step 5: Now, we will bisect the angle ZAY, using the same method as mentioned in step 3. So, we will get an angle of ${{45}^{\circ }}$ between the line AB and the bisection line of angle ZAY, which is the line AW.

Also, while solving this question, the students must ensure that they follow each and every step of construction and must take the correct measurements. And the students must mark the required points, sides and angles in the figure in order to make the construction perfect.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE





