Question

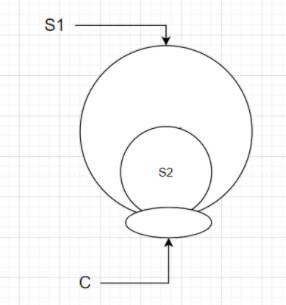
Consider two surfaces $S_1$ and $S_2$ sharing the same open circular boundary as shown in the figure. If \[{{{\theta }}_{{S_1}}}\] and \[{{{\theta }}_{{S_2}}}\]are magnetic flux through these surfaces then,

(A) \[{{{\theta }}_{{S_1}}} > {{{\theta }}_{{S_2}}}\]
(B) \[{{{\theta }}_{{S_2}}} > {{{\theta }}_{{S_1}}}\]
(C) \[{{{\theta }}_{{S_2}}} = {{{\theta }}_{{S_1}}}\]
(D) \[{{{\theta }}_{{S_1}}} = {{{\theta }}_{{S_2}}}\]

Answer 1

Hint: Magnetic flux is the number of the magnetic field passing through a closed surface. The measurement of the magnetic field actually provides the total magnetic field that passes through a given surface area.

Complete step by step answer:

Case 1:
 Since nothing is mentioned about the presence of any magnetic field producing element inside the surfaces, even if we consider C to be a closed boundary we know that that \[\phi = \oint {\overrightarrow {B.} } \overrightarrow {dS} \] but without the presence of any magnetic field producing element within the closed surface we get $\overrightarrow B = 0$ and hence the value of flux = 0
\[{{{\theta }}_{{S_1}}} = {{{\theta }}_{{S_2}}} = 0\]

Case 2:
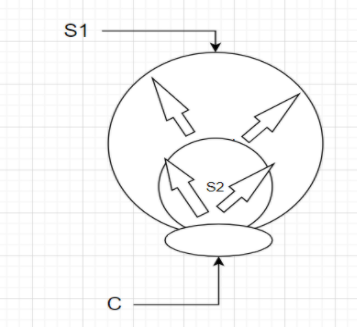
Now we consider that some flux is entering through the opening which is being shared by both the surfaces $S_1$ and $S_2$ we can notice that,
The flux that is passing through C and going through surface $S_2$ will also pass through surface $S_1$ so the flux passing through both surfaces is the same and equals net flux entering through their common circular boundary.
If we start from calculating the flux coming to $S_1$ then also we can notice that whatever the amount of flux is coming to $S_1$ that flux has come from nowhere else but the surface $S_2$. So by this approach also we can conclude that net flux passing through both the surfaces will be equal.
\[{{{\theta }}_{{S_1}}} = {{{\theta }}_{{S_2}}} = 0\]

Hence, the correct answer is option (D).

Note: In order to tackle such kinds of questions one should have understanding knowledge of the various terms involved and the application of Gauss's law. Students should have to practice a lot of numerical problems based on the application of Gauss law to master the concept behind the problems.