Question

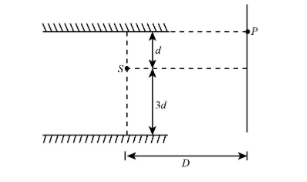
Consider the optical system shown in the figure that follows. The point source of light S is having wavelength equal to $\lambda $. The light is reaching the screen only after reflection. For point P to be 2^nd maxima the value of $\lambda $ would be ($D \gg d$ $d > \lambda $):

A $\dfrac{{12{d^2}}}{D}$
B $\dfrac{{6{d^2}}}{D}$
C $\dfrac{{3{d^2}}}{D}$
D $\dfrac{{24{d^2}}}{D}$

Answer 1

Hint:The above problem is based on the interference of the light. The value of wavelength of the light for the second maxima on the screen can be found by using the path difference of the light for both ends of the mirror. The light from the source S can reach to point P either passing from the upper end of the mirror or lower end of the mirror.

Complete step by step answer:
Given: The wavelength of the light is $\lambda $, the distance of the light source from upper end of the mirror is d, the distance of the light source from lower end of the mirror is 3d, distance of the light source S from the screen D, the number of maxima is n = 2.

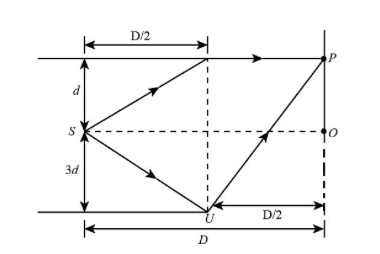
The length of the path STP is given as:
${\text{STP}} = \sqrt {{d^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \dfrac{D}{2}$
The length of the path SUP is given as:
${\text{SUV}} = \sqrt {{{\left( {3d} \right)}^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \sqrt {{{\left( {\dfrac{D}{2}} \right)}^2} + {{\left( {4d} \right)}^2}} $

The path difference for the light source is given as:
${\text{SUV}} - {\text{STP}} = \sqrt {{{\left( {3d} \right)}^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \sqrt {{{\left( {\dfrac{D}{2}} \right)}^2} + {{\left( {4d} \right)}^2}} - \sqrt {{d^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \dfrac{D}{2}$

The condition for the second maxima is given as:
${\text{SUV}} - {\text{STP}} = n\lambda $
Substitute the value of path difference and order of maxima in the above expression.
$\sqrt {{{\left( {3d} \right)}^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \sqrt {{{\left( {\dfrac{D}{2}} \right)}^2} + {{\left( {4d} \right)}^2}} - \sqrt {{d^2} + {{\left( {\dfrac{D}{2}} \right)}^2}} + \dfrac{D}{2} = 2\lambda $
Simplifying the above expression by using the binomial expression.
$2\lambda = \dfrac{{24{d^2}}}{D}$
$\lambda = \dfrac{{12{d^2}}}{D}$
Therefore, the value of the wavelength is $\dfrac{{12{d^2}}}{D}$and the option (A) is the correct answer.

Note:Use the pythagorean theorem to calculate the path of the length from both sides of the light source. The general condition of the maxima in interference path difference = $n\lambda $ to find the value of the wavelength of the light source.