Question

Consider the line $x=\sqrt{3}y$ and the circle ${{x}^{2}}+{{y}^{2}}=4$. What is the area of the region in the first quadrant enclosed by the y-axis, the line $x=\sqrt{3}$ and the circle?
A. $\dfrac{2\pi }{3}+\dfrac{\sqrt{3}}{2}$
B. $\dfrac{\pi }{2}-\dfrac{\sqrt{3}}{2}$
C. $\dfrac{\pi }{3}-\dfrac{1}{2}$
D. none of these

Answer 1

Hint: We first draw the curves of the circle and the line. We try to figure out the area which is created by the curves and the first quadrant and the Y-axis. We form the area with respect to the x function of the curves. We integrate the functions to find the solution of the problem.
We have two given equations $x=\sqrt{3}y$ and ${{x}^{2}}+{{y}^{2}}=4$. They are a line and a circle.
We first find the area enclosed by the curves and the first quadrant and the Y-axis. The area is marked with yellow colour.

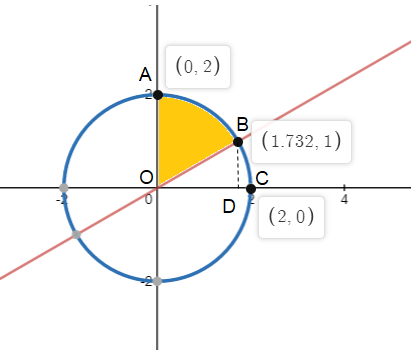
We need to find one of the cutting points of the circle with a line in the first quadrant which is point B.
We know $x=\sqrt{3}y$. Putting the value in the equation ${{x}^{2}}+{{y}^{2}}=4$ we get
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}=4 \\
 & \Rightarrow {{\left( \sqrt{3}y \right)}^{2}}+{{y}^{2}}=4 \\
 & \Rightarrow 4{{y}^{2}}=4 \\
 & \Rightarrow y=\pm 1 \\
\end{align}$
Putting the value of y in $x=\sqrt{3}y$, we get $x=\pm \sqrt{3}$.
Now we are finding the cutting point in the first quadrant where the sign of points is positive.
The point B will be $\left( \sqrt{3},1 \right)$.
Now we find the marked area we find the area covered under the circle ${{x}^{2}}+{{y}^{2}}=4$ in the interval $\left( 0,\sqrt{3} \right)$ and then subtract the area covered under the line $x=\sqrt{3}y$ in the interval $\left( 0,\sqrt{3} \right)$. We have the functions of y as functions of x where $y=\sqrt{4-{{x}^{2}}}$ for the circle and $y=\dfrac{x}{\sqrt{3}}$ for the line.
To express the mathematical form in integration we get $\int\limits_{0}^{\sqrt{3}}{\left[ \left( \sqrt{4-{{x}^{2}}} \right)-\left( \dfrac{x}{\sqrt{3}} \right) \right]}dx$.
We apply the integral formula of $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+c$.
\[\begin{align}
  & \int\limits_{0}^{\sqrt{3}}{\left[ \left( \sqrt{4-{{x}^{2}}} \right)-\left( \dfrac{x}{\sqrt{3}} \right) \right]}dx \\
 & \Rightarrow \left[ \dfrac{x}{2}\sqrt{4-{{x}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\dfrac{x}{2}-\dfrac{{{x}^{2}}}{2\sqrt{3}} \right]_{0}^{\sqrt{3}} \\
 & \Rightarrow \left[ \dfrac{\sqrt{3}}{2}\sqrt{4-3}+2{{\sin }^{-1}}\dfrac{\sqrt{3}}{2}-\dfrac{3}{2\sqrt{3}} \right]-\left[ 0 \right] \\
 & \Rightarrow \dfrac{2\pi }{3} \\
\end{align}\]

The correct option is D.

Note:
We also could have expressed the functions as functions of y but the domain would have changed accordingly. The function would have been x as functions of y where $x=\sqrt{4-{{y}^{2}}}$ for the circle and $x=\sqrt{3}y$ for the line.