Question

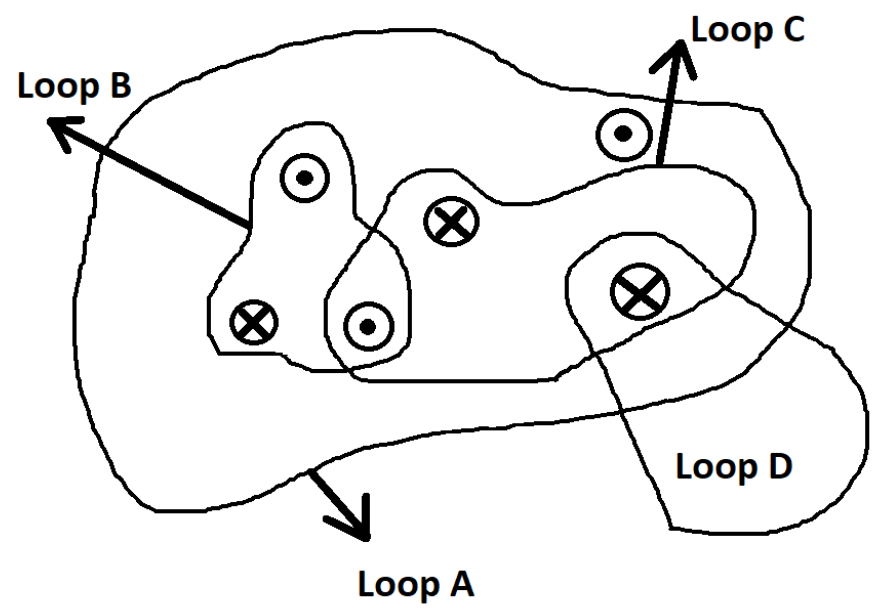
Consider six wires into or out of the page, all with the same current. Rank the line integral of the magnetic field (from most positive to most negative) taken counter-clockwise around each loop shown as positive in accordance with the right-hand screw rule.

$A. B > C > D > A$
$B. B > C = D > A$
$C. B > A > C = D$
$D. C > B = D > A$

Answer 1

Hint: This question is a simple implementation of the Ampere’s Law. The circuital law of Ampere in classical electromagnetism relates the integrated magnetic field around a closed loop to the electric current passing through the loop. It is named after the founder of this law, Andre-Marie Ampere.

Formula Used:
For solving this question, we will be using the formula for the line integral of the magnetic field according to the Ampere’s Law, i.e.,
\[\oint B.dl=\mu_0I\]

Complete step-by-step solution
For solving this question, let us go through each loop one by one,
So,
For loop A
There are three wires going outside the page (three dots in the diagram) and three of the wires are going into the page (three crosses in the diagram)
So, now by applying the Ampere’s Law,
We have,
\[\Rightarrow \oint B.dl={{\mu }_{0}}(I+I+I-I-I-I)\]
\[\Rightarrow \oint B.dl=0\]
Now,
For loop B
There are two wires going outside the page (two dots in the diagram) and one of the wires are going into the page (one crosses in the diagram)
So, now by applying the Ampere’s Law,
We have,
\[\Rightarrow \oint B.dl={{\mu }_{0}}(I+I-I)\]
\[\Rightarrow \oint B.dl={{\mu }_{0}}I\]

For loop C
There are one wire going outside the page (one dots in the diagram) and two of the wires are going into the page (two crosses in the diagram)
So, now by applying the Ampere’s Law,
\[\Rightarrow \oint B.dl={{\mu }_{0}}(I-I-I)\]
\[\Rightarrow \oint B.dl=-{{\mu }_{0}}I\]
Now,
For loop D
There is only one wire are going into the page (two crosses in the diagram)
So, now by applying the Ampere’s Law,
\[\Rightarrow \oint B.dl={{\mu }_{0}}(-I)\]
\[\Rightarrow \oint B.dl=-{{\mu }_{0}}I\]
So, on ranking the line integral of the magnetic field (from most positive to most negative)
We have,
$B > A > C = D$
So, the correct option is Option – C, i.e., B > A > C = D.

Note: The French physicist and mathematician André-Marie Ampère was one of the founders of the science of classical electromagnetism, which he referred to as electrodynamics. He is also the author of several applications, such as the solenoid and the electrical telegraph. There are many practical applications of Ampere's law. The key application is the computation of the magnetic field produced by an electrical current. This is useful for electromagnets, engines, generators, conversions, etc.