Question

Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is the same for both pebbles with respect to the disc. Assume that:
(i) they land back on the disc before the disc has completed $\dfrac{1}{8}$ rotation,
(ii) their range is less than half the disc radius, and
(iii) \[\omega \] remains constant throughout.
Then:

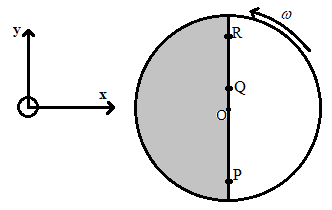
A. P lands in the shaded region and Q in the unshaded region.
B. P lands in the unshaded region and Q in the shaded region.
C. Both P and Q land in the unshaded region.
D. Both P and Q land at the edge of the shaded and unshaded region.

Answer 1

Hint: We are given a disc which rotates in a horizontal plane with a constant angular velocity about the centre of the disc. One part of the disc is shaded and the other is unshaded. The positions of two pebbles kept on the disc are shown by the figure given. By using the number of rotations we can calculate the position of the disc after the rotations and also by finding the resultant velocity of the pebbles we will get the solution.

Complete answer:
In the question we are given a circular disc which is rotating in a horizontal plane with a constant angular speed $\omega $ about the centre ‘O’ of the disc.
Two pebbles P and Q are placed simultaneously on the disc projected towards the disc as shown in the figure in the question.
It is said that the velocity of the projection is in the y – z plane for both the pebbles with respect to the disc.
In the question we are given three assumptions.
The first assumption says that the pebbles land back on the disc before the disc completes $\dfrac{1}{8}$ rotation. The second assumption says that the range is less than half the radius of the disc and the angular velocity remains constant throughout.
We know that in one rotation it completes $2\pi $ distance, therefore after $\dfrac{1}{8}$ rotation, it will complete $2\pi \times \dfrac{1}{8}=\dfrac{\pi }{4}$ distance.
Therefore we can find the time required to rotate $\dfrac{\pi }{4}$ distance will be, $\dfrac{\pi }{4\omega }$.
The figure below represents the situation when the disc rotates $\dfrac{1}{8}$ rotations.
 

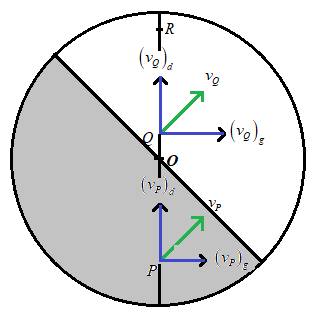
From this figure itself we can see that the pebble Q will fall in the unshaded region.
Here ‘${{\left( {{v}_{Q}} \right)}_{d}}$’ and ‘${{\left( {{v}_{Q}} \right)}_{g}}$’ are the velocities of the pebble Q with respect to the disc and ground respectively, and ‘${{v}_{Q}}$’ is the resultant velocity of the pebble Q. Similarly ‘${{\left( {{v}_{P}} \right)}_{d}}$’ and ‘${{\left( {{v}_{P}} \right)}_{g}}$’ are the velocities of the pebble P with respect to the disc and ground respectively and ‘${{v}_{P}}$’ is its resultant velocity.
We know that the pebble Q will fall in the unshaded region. So let us consider the pebble P.
We can calculate the x – coordinate of P as,
$x=v\times t$, were ‘v’ is the speed and ‘t’ is the time.
Therefore the maximum distance in the x – direction will be,
${{x}_{\max }}={{v}_{\max }}\times t$
We have time, $t=\dfrac{\pi }{4\omega }$
And we know that the velocity in circular motion is, $v=r\omega $, where ‘r’ is the radius and ‘$\omega $’ is the angular velocity.
Therefore we will get,
$\Rightarrow {{x}_{\max }}=R\omega \times \dfrac{\pi }{4\omega }$
$\Rightarrow {{x}_{\max }}=R\times \dfrac{\pi }{4}$
$\Rightarrow {{x}_{\max }}=0.785R$
Now let us see the maximum distance the pebble P can travel in the x – direction within the shaded region.

 

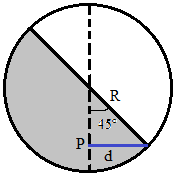
From the figure above we can see that ‘d’ is the maximum distance the pebble P can travel in the horizontal direction.
From this figure we can see that,
$\sin \left( 45 \right)=\dfrac{d}{R}$
$\Rightarrow d=R\sin \left( 45 \right)$
Since $\sin \left( 45 \right)=\dfrac{1}{\sqrt{2}}$, we will get the distance as,
$\Rightarrow d=\dfrac{R}{\sqrt{2}}$
$\Rightarrow d=0.707R$
We have the maximum distance the pebble P can travel as ${{x}_{\max }}=0.785R$ and the maximum distance the pebble P can travel in the shaded region as $d=0.707R$.
But we know that $0.785R > 0.707R$. Hence we can say that the pebble P will not fall in the shaded region.
Therefore both the pebbles P and Q will fall in the unshaded region.

So, the correct answer is “Option C”.

Note:
Motion of a particle or an object around a circular path in a fixed orbit is known as rotational motion.
Angular velocity of an object can be defined as the rate of change of some angle associated with the object with respect to some reference point. It can also be defined as the rate of change in the angular displacement with respect to time. For an object moving in a circular path about its centre the average velocity is $2\pi rad/s$.