Question

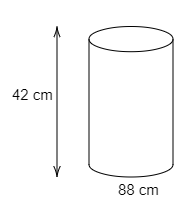
Circumference of the base of a cylinder is \[88cm\] and height of the cylinder is $42\,cm$. Find its volume.

A) $25878\,c{m^3}$
B) $28572\,c{m^3}$
C) $25870\,c{m^3}$
D) $22584\,c{m^3}$

Answer 1

Hint: Since the circumference of the base of the cylinder is given, using its equation, we can find the radius of the base of the cylinder. Remember that the base of the cylinder will be a circle. Then using the radius and the height given, we can find its volume.

Formula used:
Circumference/ Perimeter of a circle with radius $r$ is $2\pi r$.
For a cylinder with base radius $r$ and height $h$, the volume is
$V = \pi {r^2}h$

Complete step by step solution:
Given that the cylinder has a base with circumference $88cm$ and height of the cylinder is $42\,cm$.
We need to find its volume.
We know that the base of a cylinder will be a circle.
So, this circle has circumference $88cm$.
Circumference/ Perimeter of a circle with radius $r$ is $2\pi r$.
Substituting we get,
$ \Rightarrow 2\pi r = 88$
Dividing both sides by $2$ we have,
$ \Rightarrow \pi r = \dfrac{{88}}{2} = 44$
We know the value of $\pi $ can be approximated to $\dfrac{{22}}{7}$.
Using this in the above equation we have,
$ \Rightarrow \dfrac{{22}}{7}r = 44$
Multiplying both sides by $\dfrac{7}{{22}}$,
$ \Rightarrow \dfrac{{22}}{7}r \times \dfrac{7}{{22}} = 44 \times \dfrac{7}{{22}}$
Simplifying we get,
$ \Rightarrow r = 2 \times 7 = 14$
So, the radius of the base is $14cm$.
Now using this we can find the volume of the cylinder.
For a cylinder with base radius $r$ and height $h$, the volume is
$\Rightarrow V = \pi {r^2}h$
Substituting for $r,h$ we get,
$ \Rightarrow V = \pi \times {14^2} \times 42$
Again, by using the fractional approximation of $\pi $ we have,
$ \Rightarrow V = \dfrac{{22}}{7} \times 14 \times 14 \times 42$
$ \Rightarrow V = 22 \times 2 \times 14 \times 42 = 25872$
So, the volume of the cylinder is $25872\,c{m^3}$.
Since this value is not given in the options, we can choose the one nearest to it from the options, which is $25870\,c{m^3}$.

$\therefore $ Option (C) is the correct answer.

Note: Instead of the circumference given, we may also give the base area of the cylinder. In that case too, we can do it in a similar way. That is to derive radius from the base area and then calculate the volume. It is also important to add the correct units. If the radius and height are given in centimetres, then the area will be in square centimetres and volume will be in cubic centimetres.