Question

What is the cartesian form of complex numbers ?

Answer 1

Hint: The cartesian form of a complex number is represented in a two – dimensional plane . Let $$a+ib$$ be a complex number , here $$a$$ represents the real part of the complex number and $$b$$ represents the imaginary part of the complex number .

Complete step-by-step answer:
A complex number system is a form of number system in which imaginary numbers are represented . The cartesian plane of the complex number has two axes - one is the imaginary axis and the other one is the real axis . For better understanding , let us take an example :
Let $$z_1=a+ib$$ be a complex number . Let us plot it on a cartesian plane .
 

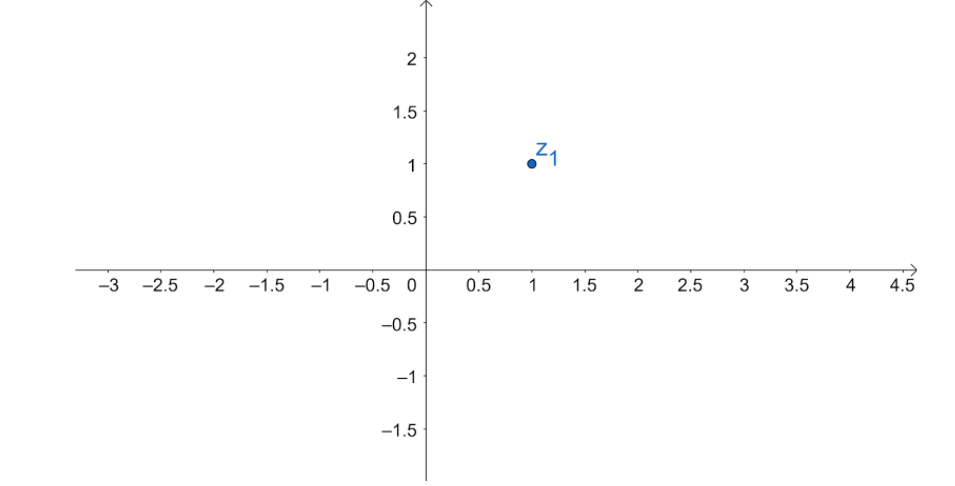
The real number is called the subset of the complex number as when we have $$b=0$$ . Also , the conjugate of a complex number can be represented on cartesian plane such as :
$$z_2=\overline{a+ib}$$ can be represented as ,

Therefore , the imaginary part will become negative after taking the conjugate of a complex number . A complex number can be represented in a Cartesian axis diagram with a real and an imaginary axis - also known as the Argand diagram .

Note: The argument of a complex number can be calculated by taking $$\tan$$ of slope of the point . The argument of $$\overline{z_1}$$ depends upon the quadrant in which point $$z_1$$ lies . The conjugate of a complex number is represented by $$\overline{z_1}$$ which is equal to $$\overline{z_1}=a-ib$$ . The plane on which a complex number is represented is also known as the Gaussian plane .