Question

By using integration prove that the area of a circle of radius r units is $\pi {{r}^{2}}$ square units

Answer 1

Hint: Use the fact that the equation of a circle of radius r centred at the origin is ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$. Observe that the curve is symmetrical in all the four quadrants. Hence find the area in the first quadrant, and hence the area of the circle will be four times the area in the first quadrant. For finding the area in the first curve quadrant express y in terms of x. Note that y>0 and hence take only the positive sign. Then use the fact that the area under the curve is given by $\int_{a}^{b}{ydx}$. Substitute suitable values of a and b and integrate and hence find the area.

Complete step-by-step answer:

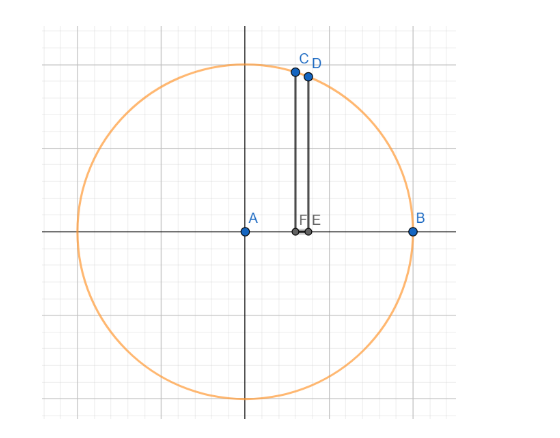
As is evident from the graph that the curve is symmetrical in the four quadrants. Hence, we will find the area in the first quadrant, and then the total area will be four times the area in the first quadrant.
Now, we have
${{x}^{2}}+{{y}^{2}}={{r}^{2}}$
Subtracting ${{x}^{2}}$ from both sides, we get
${{y}^{2}}={{r}^{2}}-{{x}^{2}}$
Hence, we have
$y=\pm \sqrt{{{r}^{2}}-{{x}^{2}}}$
Since in the first quadrant $y\ge 0$, we have
$y=\sqrt{{{r}^{2}}-{{x}^{2}}}$
Now consider the vertical strip CDEF.
Here CF = y and EF = dx.
Hence the area of the strip is ydx.
The total area in the first quadrant will be the sum of these vertical strips from A to B.
At point B, we have
y =0
Hence, we have
${{x}^{2}}={{r}^{2}}\Rightarrow x=\pm r$
Since the abscissa of B is positive, we have
$x=r$
Hence, we have
The area in the first quadrant is $\int_{0}^{r}{ydx}$
Substituting the value of y, we get
The area in the first quadrant is $\int_{0}^{r}{\sqrt{{{r}^{2}}-{{x}^{2}}}dx}$
Let $I=\int_{0}^{r}{\sqrt{{{r}^{2}}-{{x}^{2}}}dx}$
Finding the value of I:
Let x = r sint
Differentiating both sides with respect to t, we get
$\dfrac{dx}{dt}=r\cos t\Rightarrow dx=r\cos tdt$
When x = 0, we have $r\sin t=0\Rightarrow \sin t=0\Rightarrow t=0$
When x = r, we have
$r\sin t=r\Rightarrow \sin t=1\Rightarrow t=\dfrac{\pi }{2}$
Hence, we have
$I=\int_{0}^{\dfrac{\pi }{2}}{\sqrt{{{r}^{2}}-{{r}^{2}}{{\sin }^{2}}t}r\cos t}dt={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{\sqrt{1-{{\sin }^{2}}}t}\cos tdt$
We know that $1-{{\sin }^{2}}t={{\cos }^{2}}t$
Hence, we have
$I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{\sqrt{{{\cos }^{2}}t}\cos tdt}={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{\left| \cos t \right|\cos t}$
Since in the interval $\left( 0,\dfrac{\pi }{2} \right)$ cost is positive, we have $\left| \cos t \right|=\cos t$
Hence, we have
$I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}tdt}\text{ }\left( i \right)$
We know that $\int_{a}^{b}{f\left( x \right)dx}=\int_{a}^{b}{f\left( a+b-x \right)dx}$
Hence, we have
$I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}\left( \dfrac{\pi }{2}-t \right)dt}$
We know that $\cos \left( \dfrac{\pi }{2}-x \right)=\sin x$
Hence, we have
$I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{{{\sin }^{2}}t}dt\text{ }\left( ii \right)$
Adding equation (i) and equation (ii), we get
$2I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{\left( {{\sin }^{2}}t+{{\cos }^{2}}t \right)dt}$
We know that ${{\sin }^{2}}t+{{\cos }^{2}}t=1$
Hence, we have
$2I={{r}^{2}}\int_{0}^{\dfrac{\pi }{2}}{1dt}={{r}^{2}}\left( \left. t \right|_{0}^{\dfrac{\pi }{2}} \right)={{r}^{2}}\left( \dfrac{\pi }{2}-0 \right)=\dfrac{\pi {{r}^{2}}}{2}$
Dividing both sides by 2, we get
$I=\dfrac{\pi {{r}^{2}}}{4}$
Hence the area in the first quadrant is $\dfrac{\pi {{r}^{2}}}{4}$
Hence the area of the circle is $4\times \dfrac{\pi {{r}^{2}}}{4}=\pi {{r}^{2}}$
Q.E.D

Note:[1] We can directly solve I by using the fact that $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}}+C$
Hence, we have
$\begin{align}
  & I=\int_{0}^{r}{\sqrt{{{r}^{2}}-{{x}^{2}}}=\left. \dfrac{x}{2}\sqrt{{{r}^{2}}-{{x}^{2}}}+\dfrac{{{r}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{r} \right|_{0}^{r}} \\
 & =\left( \dfrac{r}{2}\sqrt{{{r}^{2}}-{{r}^{2}}}+\dfrac{{{r}^{2}}}{2}{{\sin }^{-1}}\dfrac{r}{r} \right)-\left( \dfrac{0}{2}\sqrt{{{r}^{2}}-{{0}^{2}}}+\dfrac{{{r}^{2}}}{2}{{\sin }^{-1}}\dfrac{0}{r} \right) \\
 & =\left( 0+\dfrac{{{r}^{2}}}{2}\times \dfrac{\pi }{2} \right)-\left( 0+0 \right)=\dfrac{\pi {{r}^{2}}}{4} \\
\end{align}$
Which is the same as obtained above.