Question

BCD is a quadrilateral such that AB = 5 cm, BC = 4 cm, CD = 7cm, AD = 6 cm and diagonal BD = 5 cm, then the area of the quadrilateral ABCD is $ 4\left( {3 + \sqrt 6 } \right)c{m^2} $ .
A. True
B. False

Answer 1

Hint: A quadrilateral has 4 sides. The diagonal of the quadrilateral divides it into two triangles. The total area of the quadrilateral is equal to the sum of the areas of the two triangles formed by dividing the quadrilateral by a diagonal.

Complete step-by-step answer:
We are given ABCD is a quadrilateral and AB=5cm, BC=4cm, CD=7cm, AD=6cm and BD=5cm where BD is the diagonal of ABCD.

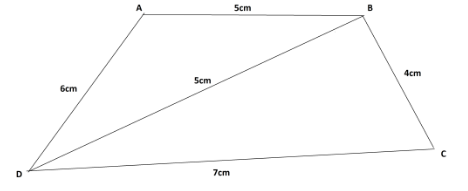
As we see in the above diagram, the diagonal of ABCD divided the quadrilateral into two triangles i.e. ABD and BDC.
We have to find the areas of these two triangles and add them together to get the area of the quadrilateral.
Area of a triangle when three sides are given is $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
In the first triangle ABD, AB=5cm, BD=5cm, AD= 6cm which means a=5cm, b=5cm, c=6cm
  $
  s = \dfrac{{a + b + c}}{2} \\
  s = \dfrac{{5 + 5 + 6}}{2} \\
  s = \dfrac{{16}}{2} \\
  s = 8cm \\
  $
Area of ABD is $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
= $
   = \sqrt {8\left( {8 - 5} \right)\left( {8 - 5} \right)\left( {8 - 6} \right)} \\
   = \sqrt {8\left( 3 \right)\left( 3 \right)\left( 2 \right)} \\
   = \sqrt {8 \times 18} \\
   = \sqrt {144} \\
   = \sqrt {{{12}^2}} \\
   = 12c{m^2} \\
  $
Therefore, area of triangle ABD is $ 12c{m^2} $
In the second triangle BDC, BD=5cm, DC=7cm, BC= 4cm which means a=5cm, b=7cm, c=4cm
  $
  s = \dfrac{{a + b + c}}{2} \\
  s = \dfrac{{5 + 7 + 4}}{2} \\
  s = \dfrac{{16}}{2} \\
  s = 8cm \\
  $
Area of BDC is $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
= $
   = \sqrt {8\left( {8 - 5} \right)\left( {8 - 7} \right)\left( {8 - 4} \right)} \\
   = \sqrt {8\left( 3 \right)\left( 1 \right)\left( 4 \right)} \\
   = \sqrt {8 \times 12} \\
   = \sqrt {96} \\
   = \sqrt {6 \times 16} \\
   = \sqrt {6 \times {4^2}} \\
   = 4\sqrt 6 c{m^2} \\
  $
Therefore, area of triangle BDC is $ 4\sqrt 6 c{m^2} $
Area of the quadrilateral ABCD = Area of the triangle ABD + Area of the triangle BDC
Area of the triangle ABD= $ 12c{m^2} $
Area of the triangle BDC= $ 4\sqrt 6 c{m^2} $
Area of the quadrilateral ABCD is
 $
   = 12 + 4\sqrt 6 \\
   = \left( {4 \times 3} \right) + 4\sqrt 6 \\
   = 4\left( {3 + \sqrt 6 } \right)c{m^2} \\
  $
Area of the quadrilateral ABCD = $ 4\left( {3 + \sqrt 6 } \right)c{m^2} $
So, the correct answer is “Option A”.

Note: A quadrilateral has four sides and it is a two-dimensional shape. Rectangle, square, parallelogram, rhombus etc are some of the examples of quadrilaterals. Sum of the interior angles of a quadrilateral is 360 °.
Area of triangle= $ \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ (Heron's formula), where $ s = \dfrac{{a + b + c}}{2} $ ; a, b, c are the three sides of the triangle.